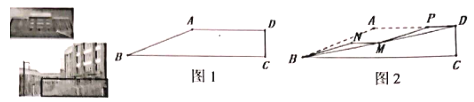
【题目】图1是我校闻澜阁前楼梯原设计稿的侧面图，
，
，楼梯
的坡比为1：
,为了增加楼梯的舒适度，将其改造成如图2，测量得
，
为
的中点，过点分别作
交
的角平分线于点
，
交
于点
，其中
和
为楼梯，
为平地，则平地的长度为_________
科目：初中数学 来源： 题型：
【题目】某校为了做好“营造清洁生活环境”活动的宣传，对本校学生进行了有关知识的测试，测试后随机抽取了部分学生的测试成绩，按“优秀、良好、及格、不及格”四个等级进行统计分析，并将分析结果绘制成如下两幅不完整的统计图：
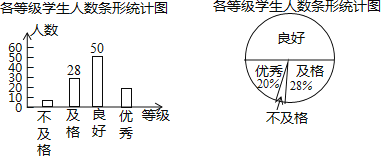
（1）求抽取的学生总人数；
（2）抽取的学生中，等级为“优秀”的人数为 人；扇形统计图中等级为“不合格”部分的圆心角的度数为 °；
（3）补全条形统计图；
（4）若该校有学生3500人，请根据以上统计结果估计成绩等级为“优秀”和“良好”的学生共有多少人．
查看答案和解析>>
科目：初中数学 来源： 题型：
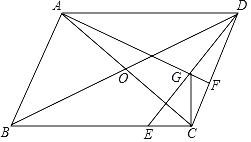
【题目】在平行四边形ABCD中，对角线AC，BD交于点O，E是BC上一点，连接DE，点F在边CD上，且AF⊥CD交DE于点G，连接CG．已知∠DEC＝45°，GC⊥BC．
（1）若∠DCG＝30°，CD＝4，求AC的长．
（2）求证：AD＝CG+
DG．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某文具店经销甲、乙两种不同的笔记本，已知：两种笔记本的进价之和为10元，甲种笔记本每本获利2元，乙种笔记本每本获利1元，小玲同学买4本甲种笔记本和3本乙种笔记本共用了47元．
(1)甲、乙两种笔记本的进价分别是多少元？
(2)该文具店购入这两种笔记本共60本，花费不超过296元，则购买甲种笔记本多少本时文具店获利最大？
查看答案和解析>>
科目：初中数学 来源： 题型：
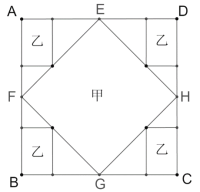
【题目】为了增加学校绿化，学校计划建造一块长为
的正方形花坛
，分别取四边中点
，构成四边形
，并计划用“两花一草”来装饰，四边形部分使用甲种花，在正方形四个角落构造4个全等的矩形区域种植乙种花，剩余部分种草坪，图纸设计如下．
（1）经了解，种植甲种花50元/
，乙种花80元/，草坪10元/，设一个矩形的面积为
，装饰总费用为
元，求关于
的函数关系式．
（2）当装饰费用为74880元时，则一个矩形区域的长和宽分别为多少?
（3）为了缩减开支，甲区域用单价为40元/的花，乙区域用单价为
元/ (
，且为10的倍数)的花，草坪单价不变，最后装饰费只用了55000元，求的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
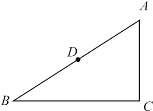
【题目】如图，在Rt△ABC中，∠C=90°，点D是AB的中点，AC＜BC．
(1)试用无刻度的直尺和圆规，在BC上作一点E，使得直线ED平分ABC的周长；(不要求写作法，但要保留作图痕迹)．
(2)在(1)的条件下，若DE分Rt△ABC面积为1﹕2两部分，请探究AC与BC的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
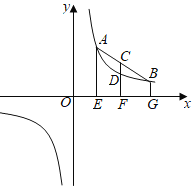
【题目】(1)阅读理解
如图，点
，
在反比例函数
的图象上，连接
，取线段的中点
．分别过点，，作
轴的垂线，垂足为
，
，
，
交反比例函数的图象于点
．点，，的横坐标分别为
，
，
．小红通过观察反比例函数的图象，并运用几何知识得出结论：AE+BG=2CF，CF>DF，由此得出一个关于
，
，
之间数量关系的命题：若
，则______．
(2)证明命题
小东认为：可以通过“若
，则
”的思路证明上述命题．
小晴认为：可以通过“若
，
，且
，则”的思路证明上述命题．
请你选择一种方法证明(1)中的命题．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一座隧道的截面由抛物线和长方形构成，长方形的长为8m，宽为2m，隧道最高点P位于AB的中央且距地面6m，建立如图所示的坐标系：
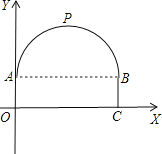
（1）求抛物线的解析式；
（2）一辆货车高4m，宽2m，能否从该隧道内通过，为什么？
（3）如果隧道内设双行道，那么这辆货车是否可以顺利通过，为什么？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
