
【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系:
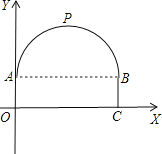
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
【答案】(1)y=﹣![]() +6;(2)货车可以通过;(3)货车可以通过.
+6;(2)货车可以通过;(3)货车可以通过.
【解析】
(1)设出抛物线的解析式,根据抛物线顶点坐标,代入解析式;(2)令y=4,解出x,然后将|x1﹣x2|与车宽2m作比较;(3)隧道内设双行道后,将(2)求出y=4时的抛物线线上两点的距离与2个车宽即4m作比较.
解:(1)由题意可知抛物线的顶点坐标(4,6),
设抛物线的方程为y=a(x﹣4)2+6,
又因为点A(0,2)在抛物线上,
所以有2=a(0﹣4)2+6.
所以a=﹣![]() .
.
因此有:y=﹣![]() +6.
+6.
(2)令y=4,则有4=﹣![]() +6,
+6,
解得x1=4+2![]() ,x2=4﹣2
,x2=4﹣2![]() ,
,
|x1﹣x2|=4![]() >2,
>2,
∴货车可以通过;
(3)由(2)可知|x1﹣x2|=![]() ,
,
∴货车可以通过.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】图1是我校闻澜阁前楼梯原设计稿的侧面图,![]() ,
,![]() ,楼梯
,楼梯![]() 的坡比为1:
的坡比为1:![]() ,为了增加楼梯的舒适度,将其改造成如图2,测量得
,为了增加楼梯的舒适度,将其改造成如图2,测量得![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 分别作
分别作![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,其中
,其中![]() 和
和![]() 为楼梯,
为楼梯,![]() 为平地,则平地
为平地,则平地![]() 的长度为_________
的长度为_________
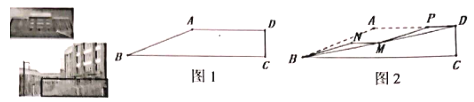
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为![]() ﹣2.其中正确的有( )
﹣2.其中正确的有( )
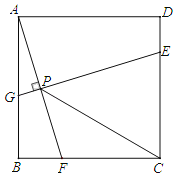
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
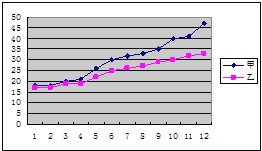
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差B.甲运动员得分的的中位数大于乙运动员得分的的中位数
C.甲运动员的得分平均数大于乙运动员的得分平均数D.甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成如图表(成绩得分均为整数):
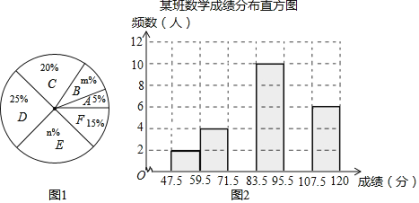
根据图表中提供的信息解答下列问题:
组别 | 成绩分组 | 频数 |
A | 47.5~59.5 | 2 |
B | 59.5~71.5 | 4 |
C | 71.5~83.5 | a |
D | 83.5~95.5 | 10 |
E | 95.5~107.5 | b |
F | 107.5~120 | 6 |
(1)频数分布表中的a= ,b= ;扇形统计图中的m= ,n= ;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 人,72分及以上为及格,预计及格的人数约为 人;
(3)补充完整频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
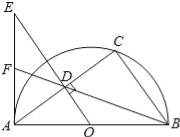
(1)求证:AEBC=ADAB;
(2)若半圆O的直径为10,sin∠BAC=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
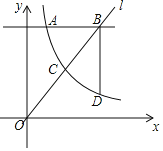
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(1)求反比例函数的解析式;
(2)当BD=2AB时,求点B的坐标;
(3)在(2)的条件下,直接写出不等式![]() >mx的解集.
>mx的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确的结论是( )
,其中正确的结论是( )
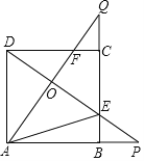
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com