
已知关于x的函数 .
.
(1)m=__________时, 是一次函数;
是一次函数;
(2)求证:对任何实数m, 的图像与
的图像与 都有公共点;
都有公共点;
(3)若是关于 的二次函数
的二次函数 的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
(4)是否存在这样的点P,使得对任何实数m, 的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
(1)根据题意得:m=0
(2)m=0 时,y=-x+1与x轴交于点(1,0)
m≠0时,△=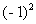 +4m(m-1)=
+4m(m-1)=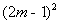 ≥0
≥0
∴对任何实数m,y=m -x-(m-1)的图像与x都有公共点;
-x-(m-1)的图像与x都有公共点;
(3) 由m -x-(m-1)=0得
-x-(m-1)=0得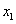 =1,
=1,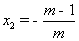 ∴AB=
∴AB=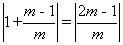
且顶点C的纵坐标
∵△ABC是等腰直角三角形
∴AB=2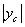 即
即
∴m=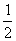 或m=
或m= ,或m=-
,或m=-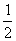
经检验m= ,或m=-
,或m=-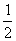
(4)由m=0得y=-x+1, m=1得y= -x
-x
由 解得
解得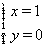 或
或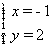 对任何实数m
对任何实数m
当x=1时,y=m -x-(m-1)=m-1-(m-1)=0
-x-(m-1)=m-1-(m-1)=0
当x=-1时,y=m -x-(m-1)=m+1-(m-1)=2
-x-(m-1)=m+1-(m-1)=2
对任何实数m,y=m -x-(m-1)的图像都经过点(1,0)(-1,2)
-x-(m-1)的图像都经过点(1,0)(-1,2)
即所求点P的坐标为(1,0)或(-1,2)


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线AB与y轴和x轴分别交于点A、点B,与反比例函数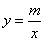 在第一象限的图象交于点C(1,6)、点D(3,n).过点C作CE⊥y轴于E,过点D作DF⊥x轴于F.
在第一象限的图象交于点C(1,6)、点D(3,n).过点C作CE⊥y轴于E,过点D作DF⊥x轴于F.
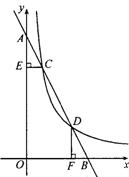 (1)求m,n的值;
(1)求m,n的值;
(2)求直线AB的函数解析式;
(3)求:△OCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
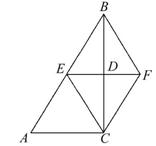
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
 ‘
‘
查看答案和解析>>
科目:初中数学 来源: 题型:
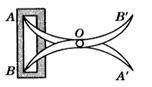
如图,将两根钢条AA′,BB′ 的中点O钉在一起,使AA′,BB′ 能绕点O自由转动,就做成一个测量工具,测A′B′ 的长即等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
A.边角边 B.角边角
C.边边边 D.斜边直角边
查看答案和解析>>
科目:初中数学 来源: 题型:
某施工队要铺设一条长为1500米的管道,为了减少施工对交通造成的影响,
施工队实际的工作效率比原计划提高了20%,结果比原计划提前2天完成任务.若设施工队原计划每天铺设管道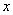 米,则根据题意所列方程正确的是( )
米,则根据题意所列方程正确的是( )
A.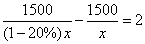 B.
B.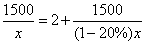
C.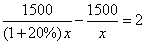 D.
D.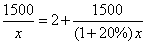
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在∠AOB的两边上截取AO=BO,OC=OD,
连接AD、BC交于点P,连接OP,则图中全等三角
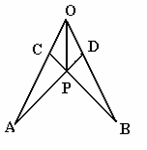 形共有( ).
形共有( ).
A. 5对 B. 4对
C. 3对 D. 2对
(
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com