
分析 (1)分别根据特殊角的三角函数值、绝对值的性质及负整数指数幂的计算法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)分别求出各不等式的解集,再求出其公共解集即可;
(3)先根据分式混合运算的法则把原式进行化简,再选取合适的a的值代入进行计算即可.
解答 解:(1)原式=2×$\frac{\sqrt{2}}{2}$+$\sqrt{2}$-2$\sqrt{2}$+3
=$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$+3
=3;
(2)$\left\{\begin{array}{l}\frac{2x-5}{3}<1①\\ 3(x-2)≥0②\end{array}\right.$,由①得,x<4,由②得,x≥2,
故不等式组的解集为:2≤x<4;
(3)原式=$\frac{3-{a}^{2}+1}{a+1}$•$\frac{a+1}{(a-2)^{2}}$
=$\frac{-(a+2)(a-2)}{a+1}$•$\frac{a+1}{{(a-2)}^{2}}$
=$\frac{-(a+2)}{a-2}$,
当a=0时,原式=$\frac{-(0+2)}{0-2}$=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
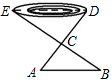 如图,为了测量一个池塘的宽DE,在岸边找一个点C,测得CD=15m,在DC的延长线上找一点A,使AC=10m,过A作AB∥DE交EC的延长线于点B,测得AB=16m,求池塘的宽DE.
如图,为了测量一个池塘的宽DE,在岸边找一个点C,测得CD=15m,在DC的延长线上找一点A,使AC=10m,过A作AB∥DE交EC的延长线于点B,测得AB=16m,求池塘的宽DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
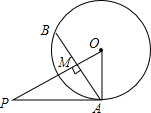 如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为( )
如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
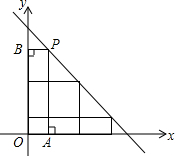 如图,在一次函数y=-x+6的图象上取一点P,作PA⊥x轴于点A,PB⊥y轴于点B,且矩形PBOA的面积为5,则在x轴的上方满足上述条件的点P的个数共有( )
如图,在一次函数y=-x+6的图象上取一点P,作PA⊥x轴于点A,PB⊥y轴于点B,且矩形PBOA的面积为5,则在x轴的上方满足上述条件的点P的个数共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
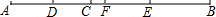 如图,已知,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点
如图,已知,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com