
分析 首先写出已知与求证,进而利用D点在圆内或D点在圆外分别证明得出即可.
解答 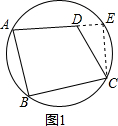 已知:四边形ABCD中,∠B+∠ADC=180°,
已知:四边形ABCD中,∠B+∠ADC=180°,
求证:四边形ABCD内接于一个圆(A,B,C,D四点共圆)
证明:如图1,假设A、B、C、D四点不共圆,过A、B、C三点作圆,D点在圆内,
延长AD与圆交于点E,连接CE,
则:∠B+∠E=180°,
∵∠ADC>∠E,
∴∠B+∠ADC>180°,
这与已知条件∠B+∠ADC=180°矛盾,故假设不成立,原结论正确,A、B、C、D四点不共圆.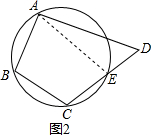 如图2,假设A、B、C、D四点不共圆,D点在圆外,
如图2,假设A、B、C、D四点不共圆,D点在圆外,
连接AE,
则:∠B+∠AEC=180°,
∵∠ADC<∠AEC,
∴∠B+∠ADC<180°,
这与已知条件∠B+∠ADC=180°矛盾,故假设不成立,原结论正确,A、B、C、D四点不共圆.
点评 此题主要考查了反证法以及四点共圆的条件,根据题意利用分类讨论得出是解题关键.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
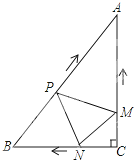 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t≤2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t≤2.5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.3×102千米 | B. | 6.3×103千米 | C. | 0.63×104千米 | D. | 630×10千米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com