
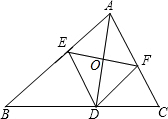
 如图,在△ABC中,AD是△ABC的角平分线,DE∥AC,DF∥AB,EF交AD于点O,请问DO是△DEF的角平分线吗?请说明理由.
如图,在△ABC中,AD是△ABC的角平分线,DE∥AC,DF∥AB,EF交AD于点O,请问DO是△DEF的角平分线吗?请说明理由. 分析 求出四边形AEDF是平行四边形,根据角平分线定义和平行线的性质求出∠EAD=∠EDA,推出AE=DE,根据菱形的判定求出四边形AEDF是菱形,根据菱形的性质得出即可.
解答 解:DO是△DEF的角平分线,
理由是:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵DE∥AC,
∴∠EDA=∠FAD,
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∴∠EAD=∠EDA,
∴AE=DE,
∴四边形AEDF是菱形,
∴AD平分∠EDF,
即DO是△DEF的角平分线.
点评 本题考查了平行四边形的判定,平行线的性质,菱形的性质和判定的应用,能求出四边形AEDF是菱形是解此题的关键,注意:菱形的每一条对角线平分一组对角.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:填空题
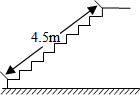 某中学要修建一座图书楼,为改善安全性能,把楼梯的倾斜角由原来设计的45°改为30°.已知原来设计的楼梯长为4.5m,在楼梯高度不变的情况下,调整后的楼梯多占地面$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m.
某中学要修建一座图书楼,为改善安全性能,把楼梯的倾斜角由原来设计的45°改为30°.已知原来设计的楼梯长为4.5m,在楼梯高度不变的情况下,调整后的楼梯多占地面$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
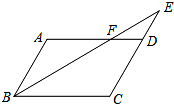 如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )
如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
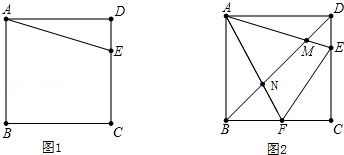
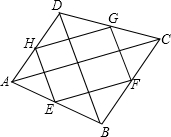 我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,E、F、G、H分别是四边形ABCD各边的中点,可证中点四边形EFGH是平行四边形,如果我们对四边形ABCD的对角线AC与BD添加一定的条件,则可使中点四边形EFGH成为特殊的平行四边形,请你经过探究后回答下面问题?
我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,E、F、G、H分别是四边形ABCD各边的中点,可证中点四边形EFGH是平行四边形,如果我们对四边形ABCD的对角线AC与BD添加一定的条件,则可使中点四边形EFGH成为特殊的平行四边形,请你经过探究后回答下面问题?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
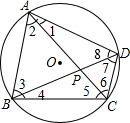 如图,圆内接四边形ABCD的对角线AC、BD把它的4个内角分成8个角,AC、BD相交于点P.
如图,圆内接四边形ABCD的对角线AC、BD把它的4个内角分成8个角,AC、BD相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com