
【题目】如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)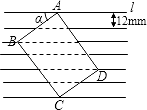
【答案】解:作BE⊥l于点E,DF⊥l于点F.
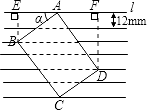
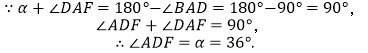
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sin ![]() ,
,
∴ ![]() mm
mm
在Rt△ADF中,cos ![]() ,
,
∴ ![]() mm.
mm.
∴矩形ABCD的周长=2(40+60)=200mm.
【解析】通过“作BE⊥l于点E,DF⊥l于点F”利用余角的性质可得出∠ADF=α=36°,利用sin36° 、cos36°的定义求出AB、BD,进而求出周长.
【考点精析】根据题目的已知条件,利用正方形的性质和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线y=kx﹣2k(k<0),与y轴交于点A,与x轴交于点B,AB=2![]() .
.

(1)直接写出点A,点B的坐标;
(2)如图2,以AB为边,在第一象限内画出正方形ABCD,求直线DC的解析式;
(3)如图3,(2)中正方形ABCD的对角线AC、BD即交于点G,函数y=mx和y=![]() (x≠0)的图象均经过点G,请利用这两个函数的图象,当mx>
(x≠0)的图象均经过点G,请利用这两个函数的图象,当mx>![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司提供的移动通讯服务的收费标准有两种套餐如表
|
| |
每月基本服务费(元) | 20 | 30 |
每月免费通话时间(分) | 100 | 150 |
每月超过免费通话时间加收通话费(元/分) | 0.4 | 0.5 |
李民选用了![]() 套餐
套餐
(1)5月份李民的通话时间为120分钟,这个月李民应付话费多少元?
(2)李民6月份的通话时间超过了150分钟,根据自己6月份的通话时间情况计算,如果自己选用![]() 套餐可以省4元钱,李民6月份的通话时间是多少分钟?
套餐可以省4元钱,李民6月份的通话时间是多少分钟?
(3)10月份李民改用了![]() 套餐,李民发现如果与9月份交相同的话费,10月份他可以多通话15分钟,李民9月份交了多少话费?
套餐,李民发现如果与9月份交相同的话费,10月份他可以多通话15分钟,李民9月份交了多少话费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,H、F分别为AD、BC边的中点,四边形EFGH为矩形,E、G分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH的面积之比为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分如图,在ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.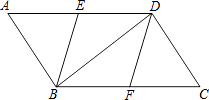
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合).
(1)如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB= °
(2)如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D
①若∠BAO=60°,则∠D= °.
②随着点A,B的运动,∠D的大小会变吗?如果不会,求∠D的度数;如果会,请说明理由.
(3)如图③,延长MO至Q,延长BA至G,已知∠BAO,∠OAG的平分线与∠BOQ的平分线及其延长线相交于点E、F,在△![]() 中,如果有一个角是另一个角的3倍,求∠ABO的度数.
中,如果有一个角是另一个角的3倍,求∠ABO的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
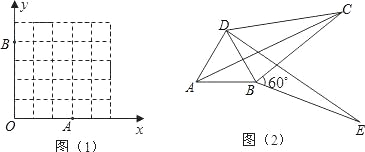
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标.
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD、DC,∠DCB=30°.求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
(4)若将图2中△ABC绕顶点B按顺时针方向旋转a度(0°<a<90°),得到△DBE,连接AD、DC,则∠DCB= °,四边形ABCD是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;

(2)补全条形统计图;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中、∠BAD=120°,点O为射线CA 上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.
(1)如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;
(2)如图②,点O在CA的延长线上,且OA=![]() AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;
AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;
(3)点O在线段AC上,若AB=6,BO=2![]() ,当CF=1时,请直接写出BE的长.
,当CF=1时,请直接写出BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com