
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпyЃНkxЉ2kЃЈkЃМ0ЃЉЃЌгыyжсНЛгкЕуAЃЌгыxжсНЛгкЕуBЃЌABЃН2![]() ЃЎ
ЃЎ

ЃЈ1ЃЉжБНгаДГіЕуAЃЌЕуBЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌвдABЮЊБпЃЌдкЕквЛЯѓЯоФкЛГіе§ЗНаЮABCDЃЌЧѓжБЯпDCЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЃЈ2ЃЉжае§ЗНаЮABCDЕФЖдНЧЯпACЁЂBDМДНЛгкЕуGЃЌКЏЪ§yЃНmxКЭyЃН![]() ЃЈxЁй0ЃЉЕФЭМЯѓОљОЙ§ЕуGЃЌЧыРћгУетСНИіКЏЪ§ЕФЭМЯѓЃЌЕБmxЃО
ЃЈxЁй0ЃЉЕФЭМЯѓОљОЙ§ЕуGЃЌЧыРћгУетСНИіКЏЪ§ЕФЭМЯѓЃЌЕБmxЃО![]() ЪБЃЌжБНгаДГіxЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌжБНгаДГіxЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈ0ЃЌ4ЃЉЃЌBЃЈ2ЃЌ0ЃЉ;ЃЈ2ЃЉyЃНЉ2x+14;ЃЈ3ЃЉЉ3ЃМxЃМ0ЛђxЃО3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнжБЯпЕФНтЮіЪНгыyжсНЛгкЕуAЃЌгыxжсНЛгкЕуBЃЌЗжБ№АбЕуAКЭЕуBгУКЌгаkЕФДњЪ§ЪНБэЪОГіРДЃЌдйИљОнAB=2![]() ЧѓГіkМДПЩЕУAЁЂBЕФзјБъЃЛ
ЧѓГіkМДПЩЕУAЁЂBЕФзјБъЃЛ
ЃЈ2ЃЉзїCHЁЭxжсгкHЃЌИљОне§ЗНаЮЕФаджЪКЭШЋЕШШ§НЧаЮЕФХаЖЈЯШЧѓжЄЁїAOBЁеЁїBHCЃЌДгЖјЕУЕНCHЃН2ЃЌBHЃН4ЃЌНјЖјЕУЕНЕуCЕФзјБъЃЌдйИљОнЦНааЯпЕФаджЪЧѓГіжБЯпCDЕФНтЮіЪНМДПЩЃЛ
ЃЈ3ЃЉЯШЧѓГідкЕквЛЯѓЯоФкНЛЕуЕФзјБъЃЌИљОнКЏЪ§ЕФаджЪКЭЭМЯѓЙлВьМДПЩЕУ.
НтЃКЃЈ1ЃЉЁпжБЯпyЃНkxЉ2kЃЈkЃМ0ЃЉЃЌгыyжсНЛгкЕуAЃЌгыxжсНЛгкЕуBЃЌ
ЁрAЃЈ0ЃЌЉ2kЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
ЁпABЃН2![]() ЃЌ
ЃЌ
Ёр4+4k2ЃН20ЃЌ
Ёрk2ЃН4ЃЌ
ЁпkЃМ0ЃЌ
ЁрkЃНЉ2ЃЌ
ЁрAЃЈ0ЃЌ4ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌзїCHЁЭxжсгкHЃЎ
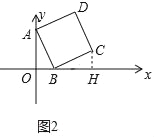
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрABЃНBCЃЌЁЯAOBЃНЁЯABCЃНЁЯBHCЃН90ЁуЃЌ
ЁрЁЯABO+ЁЯCBHЃН90ЁуЃЌЁЯCBH+ЁЯBCHЃН90ЁуЃЌ
ЁрЁЯABOЃНЁЯBCHЃЌ
ЁрЁїAOBЁеЁїBHCЃЌ
ЁрCHЃНOBЃН2ЃЌBHЃНOAЃН4ЃЌ
ЁрCЃЈ6ЃЌ2ЃЉЃЌ
ЁпCDЁЮABЃЌ
ЁрПЩвдМйЩшжБЯпCDЕФНтЮіЪНЮЊyЃНЉ2x+bЃЌАбCЃЈ6ЃЌ2ЃЉДњШыЕУЕНbЃН14ЃЌ
ЁржБЯпCDЕФНтЮіЪНЮЊyЃНЉ2x+14ЃЎ
ЃЈ3ЃЉ
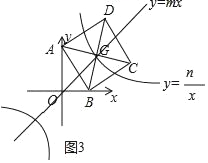
гЩAЁЂCзјБъЃЌПЩжЊдкЕквЛЯѓЯоФкНЛЕуДэБъЮЊЃЈ3,3ЃЉЙлВьЭМЯѓПЩжЊжБЯпyЃНmxгы yЃН![]() ЕФНЛЕузјБъЮЊЃЈ3ЃЌ3ЃЉЛђЃЈЉ3ЃЌЉ3ЃЉЃЌ
ЕФНЛЕузјБъЮЊЃЈ3ЃЌ3ЃЉЛђЃЈЉ3ЃЌЉ3ЃЉЃЌ
ЁрmxЃО![]() ЪБЃЌxЕФШЁжЕЗЖЮЇЮЊЉ3ЃМxЃМ0ЛђxЃО3ЃЎ
ЪБЃЌxЕФШЁжЕЗЖЮЇЮЊЉ3ЃМxЃМ0ЛђxЃО3ЃЎ


 ШЋгХПМЕфЕЅдЊМьВтОэМАЙщРрзмИДЯАЯЕСаД№АИ
ШЋгХПМЕфЕЅдЊМьВтОэМАЙщРрзмИДЯАЯЕСаД№АИ ЦЗбЇЫЋгХОэЯЕСаД№АИ
ЦЗбЇЫЋгХОэЯЕСаД№АИ аЁбЇЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аЁбЇЦкФЉГхДЬ100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк10ЁС10ЕФе§ЗНаЮЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ИіЕЅЮЛГЄЖШЃЎЁїABCЕФЖЅЕуЖМдке§ЗНаЮЭјИёЕФИёЕуЩЯЃЌЧвЭЈЙ§СНДЮЦНвЦЃЈбиЭјИёЯпЗНЯђзїЩЯЯТЛђзѓгвЦНвЦЃЉКѓЕУЕНЁї![]() ЃЌЕуCЕФЖдгІЕуЪЧжБЯпЩЯЕФИёЕу
ЃЌЕуCЕФЖдгІЕуЪЧжБЯпЩЯЕФИёЕу![]() ЃЎ
ЃЎ
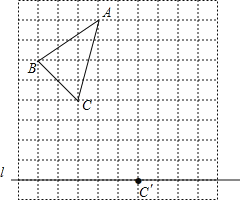
ЃЈ1ЃЉЛГіЁї![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШєСЌНг![]() ЁЂ
ЁЂ![]() ЃЌдђетСНЬѕЯпЖЮжЎМфЕФЙиЯЕЪЧЁЁ ЃЎ
ЃЌдђетСНЬѕЯпЖЮжЎМфЕФЙиЯЕЪЧЁЁ ЃЎ
ЃЈ3ЃЉЪддкжБЯп![]() ЩЯЛГіЫљгаЗћКЯЬтвтЕФИёЕуPЃЌЪЙЕУгЩЕу
ЩЯЛГіЫљгаЗћКЯЬтвтЕФИёЕуPЃЌЪЙЕУгЩЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂPЫФЕуЮЇГЩЕФЫФБпаЮЕФУцЛ§ЮЊ9ЃЎ
ЁЂPЫФЕуЮЇГЩЕФЫФБпаЮЕФУцЛ§ЮЊ9ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЕуEЁЂFЗжБ№дкБпABКЭCDЩЯЃЌЯТСаЬѕМўВЛФмХаЖЈЫФБпаЮDEBFвЛЖЈЪЧЦНааЫФБпаЮЕФЪЧЃЈЁЁЁЁЃЉ

A. AEЃНCF B. DEЃНBF C. ЁЯADEЃНЁЯCBF D. ЁЯAEDЃНЁЯCFB
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCЕФШ§БпГЄЗжБ№ЮЊaЃЌbЃЌcЃЌЯТСаЬѕМўЃКЂйЁЯA=ЁЯB-ЁЯCЃЛЂкЁЯAЃКЁЯBЃКЁЯC=3ЃК4ЃК5ЃЛЂлa2=ЃЈb+cЃЉЃЈb-cЃЉЃЛЂмaЃКbЃКc=5ЃК12ЃК13ЃЌЦфжаФмХаЖЯЁїABCЪЧжБНЧШ§НЧаЮЕФИіЪ§гаЃЈ ЃЉ
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙКТђЁАЛЦН№1КХЁБЭѕУзжжзгЃЌЫљИЖПюН№ЖюyдЊгыЙКТђСПxЃЈЧЇПЫЃЉжЎМфЕФКЏЪ§ЭМЯѓгЩЯпЖЮOAКЭЩфЯпABзщГЩЃЌдђЙКТђ1ЧЇПЫЁАЛЦН№1КХЁБгёУзжжзгашИЖПю___дЊЃЌЙКТђ4ЧЇПЫЁАЛЦН№1КХЁБгёУзжжзгаш___дЊЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁбOЕФФкНгЮхБпаЮABCDEжаЃЌЁЯB+ЁЯE=215ЁуЃЌдђЁЯCAD=ЁуЃЎ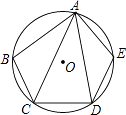
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y1=aЃЈxЉ2ЃЉ2+kжаЃЌКЏЪ§y1гыздБфСПxЕФВПЗжЖдгІжЕШчБэЃК
x | Ё | 1 | 2 | 3 | 4 | Ё |
y | Ё | 2 | 1 | 2 | 5 | Ё |
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌАбвЛеХГЄЗНаЮПЈЦЌABCDЗХдкУПИёПэЖШЮЊ12mmЕФКсИёжНжаЃЌЧЁКУЫФИіЖЅЕуЖМдкКсИёЯпЩЯЃЌвбжЊЁЯІС=36ЁуЃЌЧѓГЄЗНаЮПЈЦЌЕФжмГЄЃЎЃЈОЋШЗЕН1mmЃЉЃЈВЮПМЪ§ОнЃКsin36ЁуЁж0.60ЃЌcos36ЁуЁж0.80ЃЌtan36ЁуЁж0.75ЃЉ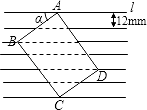
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com