
【题目】抛物线y=ax2﹣2ax﹣3a图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,顶点M的纵坐标为4,直线MD⊥x轴于点D.
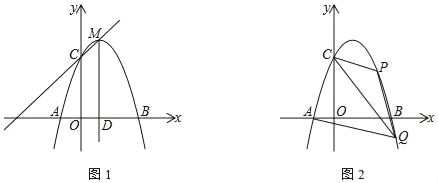
(1)求抛物线的解析式;
(2)如图1,N为线段MD上一个动点,以N为等腰三角形顶角顶点,NA为腰构造等腰△NAG,且G点落在直线CM上.若在直线CM上满足条件的G点有且只有一个时,请直接写出点N的坐标.
(3)如图,点P为第一象限内抛物线上的一点,点Q为第四象限内抛物线上一点,点Q的横坐标比点P的横坐标大1,连接PC、AQ.当PC=![]() AQ时,求S△PCQ的值.
AQ时,求S△PCQ的值.
【答案】(1)y=﹣x2+2x+3;(2)点N的坐标为(1,﹣4+2![]() )或(1,3);(3)
)或(1,3);(3)![]()
【解析】
(1)求出对称轴得到顶点坐标,代入解析式求出a值即可.
(2)当直线CM上满足条件的G点有且只有一个时,可分两种情况讨论:①NG⊥CM,且NG=NA,如图2,作CH⊥MD于H,如图2.设N(1,n),易得NG=![]() MN=
MN=![]() (4-n),NA2=22+n2=4+n2,由题可得NG=NA,由此即可得到关于n的方程,解这个方程就可解决问题;②A、N、G共线,且AN=GN,如图3,过点GT⊥x轴于T,则有AD=DT=2,运用待定系数法求出直线CM的解析式,从而得出点G的坐标,然后运用三角形的中位线定理就可解决问题.
(4-n),NA2=22+n2=4+n2,由题可得NG=NA,由此即可得到关于n的方程,解这个方程就可解决问题;②A、N、G共线,且AN=GN,如图3,过点GT⊥x轴于T,则有AD=DT=2,运用待定系数法求出直线CM的解析式,从而得出点G的坐标,然后运用三角形的中位线定理就可解决问题.
(3)根据点P在第一象限,点Q在第二象限,且横坐标相差1,进而设出点P(3-m,-m2+4m)(0<m<1);得出点Q(4-m,-m2+6m-5),得出CP2,AQ2,最后建立方程求解即可.
解:(1)将顶点M坐标(1,4)代入解析式,可得a=﹣1,抛物线解析式为y=﹣x2+2x+3
(2)当直线CM上满足条件的G点有且只有一个时,
①NG⊥CM,且NG=NA,如图1,
作CH⊥MD于H,

则有∠MGN=∠MHC=90°.
设N(1,n),
当x=0时,y=3,点C(0,3).
∵M(1,4),
∴CH=MH=1,
∴∠CMH=∠MCH=45°,
∴NG=![]() MN=
MN=![]() (4﹣n).
(4﹣n).
在Rt△NAD中,
∵AD=DB=2,DN=n,
∴NA2=22+n2=4+n2.
则![]() (4﹣n)2=4+n2
(4﹣n)2=4+n2
整理得:n2+8n﹣8=0,
解得:n1=﹣4+2![]() ,n2=﹣4﹣2
,n2=﹣4﹣2![]() (舍负),
(舍负),
∴N(1,﹣4+2![]() ).
).
②A、N、G共线,且AN=GN,如图2.
过点GT⊥x轴于T,
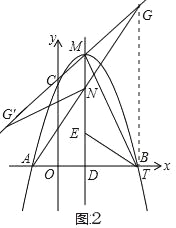
则有DN∥GT,
根据平行线分线段成比例可得AD=DT=2,
∴OT=3.
设过点C(0,3)、M(1,4)的解析式为y=px+q,
则,解得,
∴直线CM的解析式为y=x+3.
当x=3时,y=6,
∴G(3,6),GT=6.
∵AN=NG,AD=DT,
∴ND=GT=3,
∴点N的坐标为(1,3).
综上所述:点N的坐标为(1,﹣4+2![]() )或(1,3).
)或(1,3).
(3)如图3,过点P作PD⊥x轴交CQ于D,
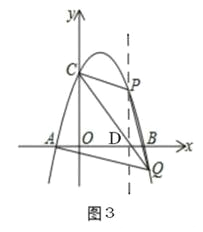
设P(3﹣m,﹣m2+4m)(0<m<1);∵C(0,3),
∴PC2=(3﹣m)2+(﹣m2+4m﹣3)2=(m﹣3)2[(m﹣1)2+1],
∵点Q的横坐标比点P的横坐标大1,
∴Q(4﹣m,﹣m2+6m﹣5),
∵A(﹣1,0).
∴AQ2=(4﹣m+1)2+(﹣m2+6m﹣5)2=(m﹣5)2[(m﹣1)2+1]
∵PC=![]() AQ,
AQ,
∴81PC2=25AQ2,
∴81(m﹣3)2[(m﹣1)2+1]=25(m﹣5)2[(m﹣1)2+1],
∵0<m<1,
∴[(m﹣1)2+1]≠0,
∴81(m﹣3)2=25(m﹣5)2,
∴9(m﹣3)=±5(m﹣5),
∴m=![]() 或m=
或m=![]() (舍),
(舍),
∴P(![]() ,
,![]() ),Q(
),Q(![]() ,﹣
,﹣![]() ),
),
∵C(0,3),
∴直线CQ的解析式为y=﹣![]() x+3,
x+3,
∵P(![]() ,
,![]() ),
),
∴D(![]() ,
,![]() ),
),
∴PD=![]() +
+![]() =
=![]()
∴S△PCQ=S△PCD+S△PQD=![]() PD×xP+
PD×xP+![]() PD×(xQ﹣xP)=
PD×(xQ﹣xP)=![]() PD×xQ=
PD×xQ=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的交点
轴的交点![]() 与
与![]() 轴交于点
轴交于点![]() .
.
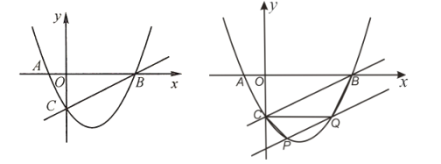
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,过点
下方抛物线上的一点,过点![]() 作
作![]() 的平行线交抛物线于点
的平行线交抛物线于点![]() (点
(点![]() 在点
在点![]() 右侧),连结
右侧),连结![]() 、
、![]() ,当
,当![]() 的面积为
的面积为![]() 面积的一半时,求
面积的一半时,求![]() 点的坐标;
点的坐标;
(3)现将该抛物线沿射线![]() 的方向进行平移,平移后的抛物线与直线
的方向进行平移,平移后的抛物线与直线![]() 的交点为
的交点为![]() 、
、![]() (点
(点![]() 在点
在点![]() 的下方),与
的下方),与![]() 轴的右侧交点为
轴的右侧交点为![]() ,当
,当![]() 与
与![]() 相似,求出点
相似,求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ;
;

(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 在第四象限的抛物线上,连接
在第四象限的抛物线上,连接![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
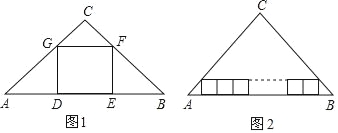
【题目】在△ABC中,∠C=90°,AC=4,BC=3,如图1,四边形DEFG为△ABC的内接正方形,则正方形DEFG的边长为_____.如图2,若三角形ABC内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
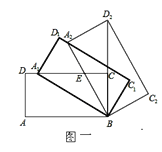
【题目】如图一,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若![]() ,求
,求![]() 的值.
的值.
(3)如图二,在(2)的条件下,直线AB上有一点P,BP=2,点E是直线DC上一动点,在BE左侧作矩形BEFG且始终保持![]() ,设AB=
,设AB=![]() ,试探究点E移动过程中,PF是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.
,试探究点E移动过程中,PF是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某段地铁工程由甲、乙两工程队合作![]() 天可完成.若单独施工,甲工程队比乙工程队多用
天可完成.若单独施工,甲工程队比乙工程队多用![]() 天.
天.
![]() 求甲、乙两工程队单独完成此项工程各需要多少天?
求甲、乙两工程队单独完成此项工程各需要多少天?
![]() 如果甲工程队施工每天需付施工费
如果甲工程队施工每天需付施工费![]() 万元,乙工程队施工每天需付施工费
万元,乙工程队施工每天需付施工费![]() 万元,甲工程队最多要单独施工多少天后,再由甲.乙两工程队合作施工完成剩下的工程,才能使施工费不超过
万元,甲工程队最多要单独施工多少天后,再由甲.乙两工程队合作施工完成剩下的工程,才能使施工费不超过![]() 万元?
万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
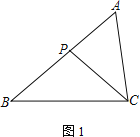
【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
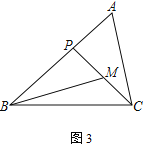
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是作一个角的角平分线的方法:以![]() 的顶点
的顶点![]() 为圆心,以任意长为半径画弧,分别交
为圆心,以任意长为半径画弧,分别交![]() 于
于![]() 两点,再分别以
两点,再分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作画弧,两条弧交于点
长为半径作画弧,两条弧交于点![]() ,作射线
,作射线![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com