Question

【题目】如图1，长方形ABCD中，∠DAB＝∠B＝∠DCB＝∠D＝90°，AD＝BC＝6，AB＝CD＝10．点E为射线DC上的一个动点，把△ADE沿直线AE翻折得△AD′E．

（1）当D′点落在AB边上时，∠DAE＝　 　°；

（2）如图2，当E点与C点重合时，D′C与AB交点F，

①求证：AF＝FC；②求AF长．

（3）连接D′B，当∠AD′B＝90°时，求DE的长．

Answer 1

【答案】（1）45；（2）①见解析；②AF＝6.8；（3）DE＝2或18．

【解析】

（1）由△ADE≌△AD′E知∠DAE＝∠D′AE，结合D′点落在AB边上知∠DAE+∠D′AE＝90°，从而得出答案；

（2）①由折叠得出∠ACD＝∠ACD′，再由AB∥CD得出∠ACD＝∠BAC，从而得知∠ACD′＝∠BAC，据此即可得证；

②设AF＝FC＝x，则BF＝10﹣x，在Rt△BCF中，由BF2+BC2＝CF2得到关于x的方程，解之可得；

（3）分两种情况：点E在DC线段上，点E为DC延长线上的一点，进一步分析探讨得出答案即可．

解：（1）由题意知△ADE≌△AD′E，

∴∠DAE＝∠D′AE，

∵D′点落在AB边上时，∠DAE+∠D′AE＝90°，

∴∠DAE＝∠D′AE＝45°，

故答案为：45；

（2）①如图2，由题意知∠ACD＝∠ACD′，

∵四边形ABCD是矩形，

∴AB∥CD，

∴∠ACD＝∠BAC，

∴∠ACD′＝∠BAC，

∴AF＝FC；

②设AF＝FC＝x，则BF＝10﹣x，

在Rt△BCF中，由BF2+BC2＝CF2得（10﹣x）2+62＝x2，

解得x＝6.8，即AF＝6.8；

（3）如图3，

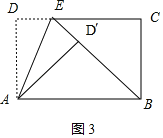
∵△AD′E≌△ADE，

∴∠AD′E＝∠D＝90°，

∵∠AD′B＝90°，

∴B、D′、E三点共线，

又∵△ABD′∽△BEC，AD′＝BC，

∴△ABD′≌△BEC，

∴BE＝AB＝10，

∵BD′＝＝＝8，

∴DE＝D′E＝10﹣8＝2；

如图4，

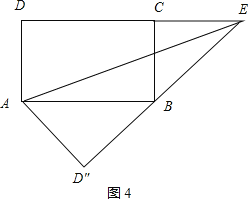
∵∠ABD″+∠CBE＝∠ABD″+∠BAD″＝90°，

∴∠CBE＝∠BAD″，

在△ABD″和△BEC中，

∵，

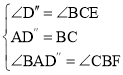∴△ABD″≌△BEC，

∴BE＝AB＝10，

∴DE＝D″E＝8+10＝18．

综上所知，DE＝2或18．