
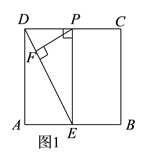
【题目】边长为2的正方形ABCD中E是AB的中点,P在射线DC上从D出发以每秒1个单位长度的速度运动,过P做PF⊥DE,当运动时间为__________秒时,以点P、F、E为顶点的三角形与△AED相似

【答案】1或![]()
【解析】∵四边形ABCD是正方形,PF⊥DE,
∴∠A=∠DFP=∠ADC=90°,
∴∠ADE+∠EDP=∠EDP+∠DPF=90°,
∴∠ADE=∠FPD,
∴△ADE∽△FPD.
(1)如图1,当∠DPE=90°时,易得△FPD∽△FEP,则△ADE∽△FEP,
此时四边形AEPD是矩形,
∴DP=AE=1,
∴t=1,即当t=1时,△ADE∽△FEP;
(2)如图2,当DP=EP时,易得△FPE≌△FPD,则△FEP∽△ADE,
此时四边形AEHD是矩形,
∴DH=AE=1,HP=x-1,HE=AD=2,
∴PE2=HE2+HP2=PD2,
∴![]() ,解得:
,解得: ![]() ;
;

综上所述,当![]() 或
或![]() 时,以点P、F、E为顶点的三角形与△AED相似.
时,以点P、F、E为顶点的三角形与△AED相似.
故答案为:1或![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
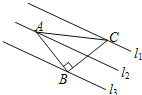
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.
(1)设经过的时间为t秒,则用含t的代数式表示甲的路程为 米;
(2)当甲、乙两人第一次相遇时,求所经过的时间t为多少秒?
(3)若甲改为沿着A-B-C-D-A的方向循环跑步,而乙仍按原来的方向跑步,两人的速度不变,求经过多少秒,乙追上甲?
(4)在(3)的条件下,当乙第一次追上甲后继续跑步,则最少再经过![]() 秒乙又追上甲,这时两人所处的位置在点P;直接写出
秒乙又追上甲,这时两人所处的位置在点P;直接写出![]() 的值,在图中标出点P,不要求书写过程.
的值,在图中标出点P,不要求书写过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
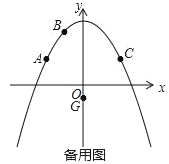
【题目】二次函数y=ax2+c的图象经过点A(﹣4,3),B(﹣2,6),点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点G(0,﹣1).
(1)求出点C坐标及抛物线的解析式;
(2)若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
(3)若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将△QGM沿QG翻折得到△QGN,当点N在坐标轴上时,求Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形ABCD中,∠DAB=∠B=∠DCB=∠D=90°,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,把△ADE沿直线AE翻折得△AD′E.

(1)当D′点落在AB边上时,∠DAE= °;
(2)如图2,当E点与C点重合时,D′C与AB交点F,
①求证:AF=FC;②求AF长.
(3)连接D′B,当∠AD′B=90°时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.


第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按规律排列的一列式子:
第1个式子:![]() ;
;
第2个式子: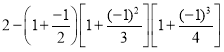 ;
;
第3个式子: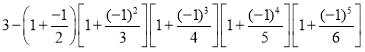 ;
;
……
(1)分别计算出这三个式子的结果;
(2)请按规律写出第2019个式子的形式(中间部分用省略号,两端部分必须写详细);
(3)计算第2019个式子的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com