【题目】如图，矩形
中，
为
中点，过点的直线分别与
，
交于点
，
，连结
，交于点
，连结
，
．若
，
，则下列结论：①
；②垂直平分线段
；③
；④四边形是
菱形．其中正确结论的个数是（ ）
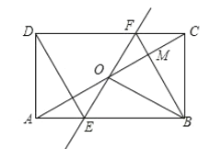
A.1个B.2个C.3个D.4个
【答案】C
【解析】
通过证△AEO≌CFO可判断①；利用矩形的性质证△OCB是正三角形，可得②；因OB≠MB，得到③错误；通过证△EOB≌△FCB得到EB=FB，从而证④．
∵四边形ABCD是矩形
∴AB∥DC,AO=OC
∴∠AEO=∠CFO,∠EAO=∠FCO
∴△AEO≌CFO(AAS)
∴AE=FC，①正确
∵四边形ABCD是矩形
∴OC=OB
∵∠BOC=60°
∴△OCB是正三角形，∴OB=OC
∵FO=FC
∴FB是线段OC的垂直平分线，②正确
∵BM⊥OC，∴△OMB是直角三角形，∴OB＞BM
∴
是错误的，即③错误
∵四边形ABCD是矩形
∴EB∥DF，AB=DC
∵AE=FC
∴EB=DF
∴四边形EBFD是平行四边形
∵△AEO≌△CFO，OF=FC，∴AE=EO=OF=FC
∵△OBC是正三角形，∴∠BOC=60°=∠BCO，BC=BO
∴∠FCO=30°，∴∠FOC=30°
∴∠FOB=30°+60°=90°
∴∠EOB=90°=∠FCB
∴△EOB≌△FCB(SAS)
∴EB=FB
∴平行四边形EBFD是菱形，④正确
故选：C
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2；
（2）若将△A1B1C绕某一点旋转可以得到△A2B2C2；请在图中标明旋转中心P的位置并写出其坐标．
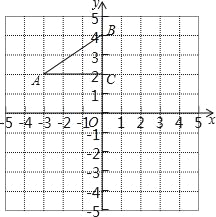
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解青少年形体情况，现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况（如果一个学生有一种以上不良姿势，以他最突出的一种作记载），并将统计结果绘制了如下两幅不完整的统计图，请根据图中所给信息解答下列问题：
（1）求这次被抽查形体测评的学生一共有多少人？
（2）求在被调查的学生中三姿良好的学生人数，并将条形统计图补充完整；
（3）若全市有5万名初中生，那么估计全市初中生中，坐姿和站姿不良的学生共有多少人？
【答案】（1）500名；（2）75名；（3）2.5万
【解析】试题分析：（1）用类型人数除以所占百分比就是总人数.(2)用总人数乘以15%.
(3) 坐姿和站姿不良的学生的学生的百分比乘以总人数.
试题解析：
（1）解：100÷20%=500（名），
答：这次被抽查形体测评的学生一共是500名；
（2）解：三姿良好的学生人数：500×15%=75名，
补全统计图如图所示；
（3）解：5万×（20%+30%）=2.5万，
答：全市初中生中，坐姿和站姿不良的学生有2.5万人．
【题型】解答题
【结束】
24
【题目】如图，矩形ABCD中，P为AD边上一点，沿直线BP将△ABP翻折至△EBP（点A的对应点为点E），PE与CD相交于点O，且OE=OD．
（1）求证：PE=DH；
（2）若AB=10，BC=8，求DP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在□ABCD，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF.
（1）求证：四边形BFDE是矩形；
（2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB.
查看答案和解析>>
科目：初中数学 来源： 题型：
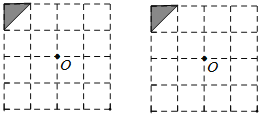
【题目】(1)如图是一个4×4的正方形网格，每个小正方形的边长均为1.请在网格中以左上角的三角形为基本图形，通过平移、对称或旋转，设计两个精美图案，使其满足：①既是轴对称图形，又能以点
为旋转中心旋转而得到；②所作图案用阴影标识，且阴影部分面积为4.
(2)如图，
的三个顶点和点都在正方形网格的格点上，每个小正方形的边长都为1.
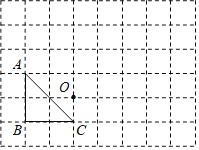
①将先向右平移4个单位，再向上平移2个单位得到
，请画出；
②请画出
，使和关于点成中心对称；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．
（1）求饮用水和蔬菜各有多少件？
（2）现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；
（3）在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点C，D在圆上，且四边形AOCD是平行四边形，过点D作⊙O的切线，分别交OA的延长线与OC的延长线于点E，F，连接BF.
（1）求证：BF是⊙O的切线；
（2）已知圆的半径为1，求EF的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某电器商场销售A、B两种型号计算器，两种计算器的进货价格分别为每台30元，40元，商场销售5台A型号和1台B型号计算器，可获利润76元；销售6台A型号和3台B型号计算器，可获利润120元．求商场销售A、B两种型号计算器的销售价格分别是多少元？（利润=销售价格﹣进货价格）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：直线EF//MN，点A、B分别为EF，MN上的动点，且∠ACB= a，BD平分∠CBN交EF于D．
（1）若∠FDB=120°，a=90°．如图1，求∠MBC与∠EAC的度数？
（2）延长AC交直线MN于G，这时a =80°，如图2，GH平分∠AGB交DB于点H，问∠GHB是否为定值，若是，请求值．若不是，请说明理由？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com