
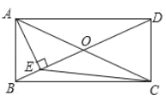
【题目】如图,在矩形![]() 中,对角线
中,对角线![]() 、
、![]() 交于
交于![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,那么
,那么![]() 的面积是( )
的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
过点C作CF⊥BD于F.根据矩形的性质得到∠ABE=∠CDF=60°,AB=CD,AD=BC=2,∠AEB=∠CFD=90°.根据全等三角形的性质得到AE=CF.解直角三角形得到OE=![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
解:如图:过点C作CF⊥BD于F.
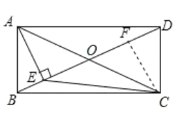
∵矩形ABCD中,BC=2,AE⊥BD,
∴∠ABE=∠CDF=60°,AB=CD,AD=BC=2,∠AEB=∠CFD=90°.
∴△ABE≌△CDF,(AAS),
∴AE=CF.
∵∠ABE=∠CDF=60°,
∴∠ADE=∠CBF=30°,
∴CF=AE=![]() AD=1,
AD=1,
∴BE=![]() =
=![]() AE=
AE=![]() ,
,
∵∠ABE=60°,AO=BO,
∴△ABO是等边三角形,
∴OE=BE=![]() ,
,
∴S△ECO=![]() OECF=
OECF=![]() ,
,
故选:B.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象的对称轴是直线
的图象的对称轴是直线![]() ,则下列理论:①
,则下列理论:①![]() ,
, ![]() ②
②![]() ,③
,③![]() ,④
,④![]() ,⑤当
,⑤当![]() 时,
时, ![]() 随
随![]() 的增大而减小,其中正确的是( ).
的增大而减小,其中正确的是( ).

A. ①②③ B. ②③④ C. ③④⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
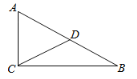
【题目】如图,Rt△ABC中,∠ACB=90°,AC=9,BC=12,D是AB边的中点,P是BC边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与△ABC相似,则线段PC=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
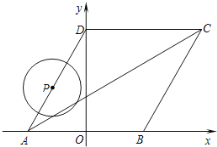
【题目】如图所示,菱形ABCD的顶点A、B在![]() 轴上,点A在点B的左侧,点D在
轴上,点A在点B的左侧,点D在![]() 轴的正半轴上,
轴的正半轴上,![]() ,点A的坐标为
,点A的坐标为![]() .
.
(1)求D点的坐标.
(2)求直线AC的函数关系式.
(3)动点P从点A出发,以每秒1个单位长度的速度,按照![]() 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为![]() 秒.求
秒.求![]() 为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
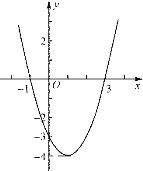
(1)写出方程ax2+bx+c=0(a≠0)的实数解;
(2)若方程ax2+bx+c=k有两个不相等的实数根,写出 k的取值范围;
(3)当0<x<3 时,写出函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.
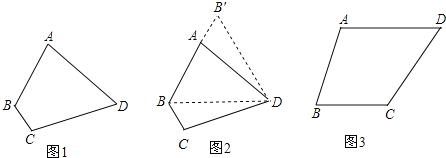
【尝试解决】
旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,则△BDB′的形状是 .
(2)在(1)的基础上,求四边形ABCD的面积.
[类比应用]如图3,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=2,BC=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
考点:几何变换综合题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:对于关于![]() 的函数
的函数![]() ,我们称函数
,我们称函数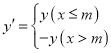 为函数y的m分函数(其中m为常数).
为函数y的m分函数(其中m为常数).
例如:对于关于x一次函数![]() 的
的![]() 分函数为
分函数为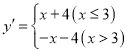
(1)若点![]() 在关于x的一次函数
在关于x的一次函数![]() 的
的![]() 分函数上,求
分函数上,求![]() 的值;
的值;
(2)写出反比例函数![]() 的
的![]() 分函数的图象上y随x的增大而减小的x的取值范围: ;
分函数的图象上y随x的增大而减小的x的取值范围: ;
(3)若![]() 是二次函数
是二次函数![]() 关于x的
关于x的![]() 分函数,
分函数,
①当![]() 时,求y的取值范围;
时,求y的取值范围;
②当![]() 时,
时,![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
③若点![]() ,连结
,连结![]() ,当关于
,当关于![]() 的二次函数
的二次函数![]() 的
的![]() 分函数,与线段MN有两个交点,直接写出m的取值范围.
分函数,与线段MN有两个交点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点M以每秒1cm的速度从点B向点C移动;同时动点N以3cm的速度从点C向A移动,当点N到达点A时,两点都停止移动,连接MN,设移动时间为t秒.
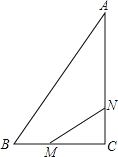
(1)当t为何值时,S△MNC=S四边形ABMN?
(2)当t为何值时,△MNC与△ABC相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com