
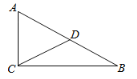
【题目】如图,Rt△ABC中,∠ACB=90°,AC=9,BC=12,D是AB边的中点,P是BC边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与△ABC相似,则线段PC=__________.
【答案】6或![]()
【解析】
由Rt△ABC中,∠ACB=90°,AC=9,BC=12,D是AB边的中点,即可求得AB与CD的值,又由以D、C、P为顶点的三角形与△ABC相似,可得∠DPC=90°或∠CDP=90°,然后根据相似三角形的对应边成比例,即可求得PC的值.
∵Rt△ABC中,∠ACB=90°,AC=9,BC=12,
∴AB=15,
∵D是AB边的中点,
∴CD=BD=![]() AB=7.5,
AB=7.5,
∵以D、C、P为顶点的三角形与△ABC相似,
∴∠DPC=90°或∠CDP=90°,
(1)如图1:
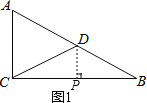
若∠DPC=90°,则DP∥AC,
∴![]() =
=![]() =
=![]() ,
,
∴BP=![]() BC=6,
BC=6,
则PC=6;
(2)如图2:
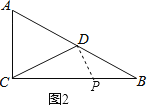
若∠CDP=90°,则△CDP∽△BCA,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴PC=![]() .
.
综上所述:PC=6或![]() .
.
故答案为:6或![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
【题目】(12分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.
(1)若商场平均每天要盈利1600元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
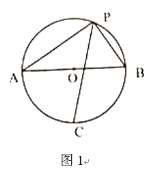
【题目】(1)已知:如图1,AB是![]() 的直径,点P为
的直径,点P为![]() 上一点(且点P不与A、B重合)连接PA,PB,
上一点(且点P不与A、B重合)连接PA,PB,![]() 的角平分线PC交
的角平分线PC交![]() 于点C.
于点C.
①若![]() ,求AB的长
,求AB的长
②求证:![]()
(2)如图2,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点B到AP的距离.
,请直接写出点B到AP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
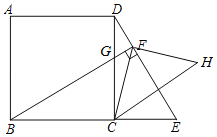
(1)求证:DGBC=DFBG;
(2)连接CF,求∠CFB的大小;
(3)作点C关于直线DE的对称点H,连接CH,FH.猜想线段DF,BF,CH之间的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读理解】
某科技公司生产一种电子产品,该产品总成本包括技术成本、制造成本、销售成本三部分。经核算,2016年该产品各部分成本所占比例约为2:a:1,且2016年该产品的技术成本、制造成本分别为400万元、1400万元。
(1)确定a的值,并求2016年产品总成本为多少万元。
(2)为降低总成本,该公司2017年及2018年增加了技术投入,确保这两年技术成本都比前一年增加一个相同的百分数m(m<50%),制造成本在这两年里都比前一年减少一个相同的百分数2m;同时为了扩大销售量,2018年的销售成本将在2016年的基础上提高10%,经过以上变革,预计2018年该产品总成本达到2016年该产品总成本的![]() 。求m的值。
。求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论k取不为1的任何值方程总有两个不相等的实数根.
(2)设![]() 是该方程的两个实数根,记
是该方程的两个实数根,记![]() ,
,![]() 的值能为1吗?若能,求出此时
的值能为1吗?若能,求出此时![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的动点
中的动点![]() 和图形
和图形![]() ,给出如下定义:如果
,给出如下定义:如果![]() 为图形
为图形![]() 上一个动点,
上一个动点,![]() ,
,![]() 两点间距离的最大值为
两点间距离的最大值为![]() ,
,![]() ,
,![]() 两点间距离的最小值为
两点间距离的最小值为![]() ,我们把
,我们把![]() 的值叫点
的值叫点![]() 和图形
和图形![]() 间的“和距离”,记作
间的“和距离”,记作![]() (
(![]() ,图形
,图形![]() ).
).
(1)如图,正方形![]() 的中心为点
的中心为点![]() ,
,![]() .
.
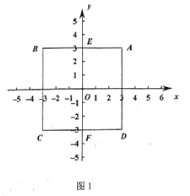
①点![]() 到线段
到线段![]() 的“和距离”
的“和距离”![]() (
(![]() ,线段
,线段![]() )=______;
)=______;
②设该正方形与![]() 轴交于点
轴交于点![]() 和
和![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() (
(![]() ,正方形
,正方形![]() )=7,求点
)=7,求点![]() 的坐标.
的坐标.
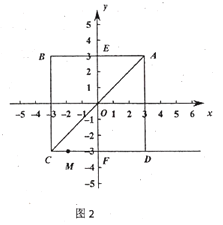
(2)如图2,在(1)的条件下,过![]() ,
,![]() 两点作射线
两点作射线![]() ,连接
,连接![]() ,点
,点![]() 是射线
是射线![]() 上的一个动点,如果
上的一个动点,如果![]() (
(![]() ,线段
,线段![]() )
)![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 取值范围.
取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com