
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论k取不为1的任何值方程总有两个不相等的实数根.
(2)设![]() 是该方程的两个实数根,记
是该方程的两个实数根,记![]() ,
,![]() 的值能为1吗?若能,求出此时
的值能为1吗?若能,求出此时![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】(1)见详解;(2)不能,见详解
【解析】
(1)利用根的判别式公式代入△=b2-4ac即可;
(2)先由根与系数关系 分别表示出x1+x2与x1x2的值,然后将代入S=x12+x22-x1x2表示为k的代数式,最后化简变形为关于k的一元二次方程进行判断即可.
解:(1)证明:△=b2-4ac=(2k)2-4(k-1)×2=4k2-8k+8=4(k2-2k)+8=4(k2-2k+1-1)+8=4(k-1)2+12,
∵4(k-1)2≥0,
∴4(k-1)2+12>0,
∴无论k取不为1的任何值,方程总有两个不相等的实数根;
(2)由根与系数关系有
![]()
∴![]()
化简得: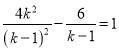
方程两边同时乘以(k-1)2得,![]() 即
即![]() ,
,
∵△=(-4)2-4×3×5<0.
∴方程无解,
∴S=x12+x22-x1x2的值不能为1.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的图象与x轴交于A(﹣3,0)、B(1,0)两点,与y轴交于点C,且OC=OA

(1)求抛物线解析式;
(2)过直线AC上方的抛物线上一点M作y轴的平行线,与直线AC交于点N.已知M点的横坐标为m,试用含m的式子表示MN的长及△ACM的面积S,并求当MN的长最大时S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为![]() 斜边AB上的一点,以OA为半径的
斜边AB上的一点,以OA为半径的![]() 与BC切于点D,与AC交于点E,连接AD.
与BC切于点D,与AC交于点E,连接AD.
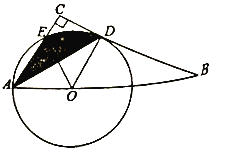
(1)求证:AD平分![]()
(2)若![]() ,
,![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
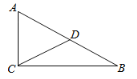
【题目】如图,Rt△ABC中,∠ACB=90°,AC=9,BC=12,D是AB边的中点,P是BC边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与△ABC相似,则线段PC=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读短文,然后回答短文后面所给出的问题:对于三个数a,b,c的平均数,最小的数都可以符号来表示,我们规定M{a,b,c}表示这三个数的平均数,min{a,b,c}表示这三个数中最小的数,max{a,b,c}表示这三个数中最大的数.例如:M{1,2,3}=![]() ,min{1,2,3}=1,max{1,2,3}=3,M{1,2,a}=
,min{1,2,3}=1,max{1,2,3}=3,M{1,2,a}=![]() =
=![]() .
.
(1)请填空:min{1,3,2}=___________.若x<0,则max{2,(x+1)2+2,x+1}=__________.
(2)若M{2x24x5,72,x2+10x7}=max{10,2x2+4x+12,8},求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
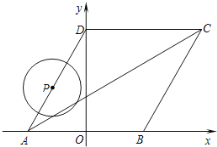
【题目】如图所示,菱形ABCD的顶点A、B在![]() 轴上,点A在点B的左侧,点D在
轴上,点A在点B的左侧,点D在![]() 轴的正半轴上,
轴的正半轴上,![]() ,点A的坐标为
,点A的坐标为![]() .
.
(1)求D点的坐标.
(2)求直线AC的函数关系式.
(3)动点P从点A出发,以每秒1个单位长度的速度,按照![]() 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为![]() 秒.求
秒.求![]() 为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
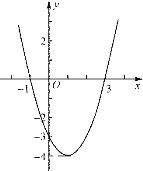
(1)写出方程ax2+bx+c=0(a≠0)的实数解;
(2)若方程ax2+bx+c=k有两个不相等的实数根,写出 k的取值范围;
(3)当0<x<3 时,写出函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
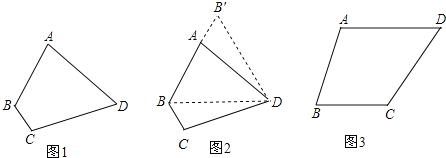
【题目】【问题提出】如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.
【尝试解决】
旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,则△BDB′的形状是 .
(2)在(1)的基础上,求四边形ABCD的面积.
[类比应用]如图3,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=2,BC=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
考点:几何变换综合题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
给出以下结论:(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;(2)当﹣![]() <x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
<x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com