
【题目】如图,点O为![]() 斜边AB上的一点,以OA为半径的
斜边AB上的一点,以OA为半径的![]() 与BC切于点D,与AC交于点E,连接AD.
与BC切于点D,与AC交于点E,连接AD.
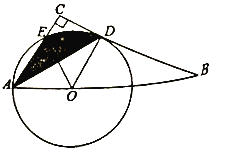
(1)求证:AD平分![]()
(2)若![]() ,
,![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() )
)
【答案】(1)见解析;(2)![]()
【解析】
(1)由Rt![]() 中,
中,![]() ,
,![]() 切BC于D,易证得AC∥OD,由半径相等可证得∠OAD=∠ADO,继而证得AD平分∠CAB;
切BC于D,易证得AC∥OD,由半径相等可证得∠OAD=∠ADO,继而证得AD平分∠CAB;
(2)如图,连接ED,根据(1)中AC∥OD和菱形的判定和性质得到四边形AEDO是菱形,则△AEM≌△DMO,则图中阴影部分的面积=扇形EOD的面积.
(1)证明:∵![]() 切BC于D,
切BC于D,
∴OD⊥BC,
∵AC⊥BC,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠CAD,
即AD平分∠CAB;
(2)设EO与AD交于点M,连接ED.
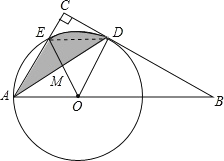
∴∠B=30°,
∴∠BAC=60°,
∵OA=OE,
∴△AEO是等边三角形,
∴AE=OA,∠AOE=60°,
∴AE=AO=OD,
又由(1)知,AC∥OD即AE∥OD,
∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,
∴![]() ,
,
∴![]() .
.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)证明:不论![]() 取何值,该函数图像与
取何值,该函数图像与![]() 轴总有公共点;
轴总有公共点;
(2)若该函数的图像与![]() 轴交于点(0,3),求出顶点坐标并画出该函数图像;
轴交于点(0,3),求出顶点坐标并画出该函数图像;
(3)在(2)的条件下,观察图像,解答下列问题:
①不等式![]() 的的解集是 ;
的的解集是 ;
②若一元二次方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是 ;
的取值范围是 ;
③若一元二次方程![]() 在
在![]() 的范围内有实数根,则
的范围内有实数根,则![]() 的取
的取
值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛,射击队对两人的射击技能进行了测评.在相同的条件下,两人各打靶5次,成绩统计如下:

(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
(2)根据以上信息,若选派一名队员参赛,你认为应选哪名队员,并说明理由.
(3)如果标标再射击1次,命中8环,那么他射击成绩的方差会 .(填“变大”“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.
(1)若商场平均每天要盈利1600元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
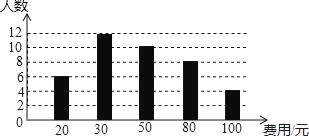
【题目】在全民读书月活动中,某校随机调查了部分同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题.
(1)这次调查获取的样本容量是 .(直接写出结果)
(2)这次调查获取的样本数据的众数是 ,中位数是 .(直接写出结果)
(3)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
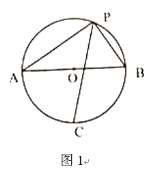
【题目】(1)已知:如图1,AB是![]() 的直径,点P为
的直径,点P为![]() 上一点(且点P不与A、B重合)连接PA,PB,
上一点(且点P不与A、B重合)连接PA,PB,![]() 的角平分线PC交
的角平分线PC交![]() 于点C.
于点C.
①若![]() ,求AB的长
,求AB的长
②求证:![]()
(2)如图2,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点B到AP的距离.
,请直接写出点B到AP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
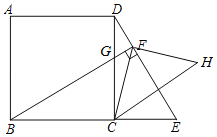
(1)求证:DGBC=DFBG;
(2)连接CF,求∠CFB的大小;
(3)作点C关于直线DE的对称点H,连接CH,FH.猜想线段DF,BF,CH之间的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论k取不为1的任何值方程总有两个不相等的实数根.
(2)设![]() 是该方程的两个实数根,记
是该方程的两个实数根,记![]() ,
,![]() 的值能为1吗?若能,求出此时
的值能为1吗?若能,求出此时![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com