
【题目】如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点M以每秒1cm的速度从点B向点C移动;同时动点N以3cm的速度从点C向A移动,当点N到达点A时,两点都停止移动,连接MN,设移动时间为t秒.
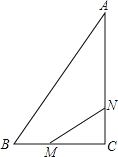
(1)当t为何值时,S△MNC=S四边形ABMN?
(2)当t为何值时,△MNC与△ABC相似?
【答案】(1)t=2;(2)t为![]() 或
或![]()
【解析】
(1)由题意可知:CM=6﹣t,CN=3t,因为S△MNC=S四边形ABMN,所以S△MNC是△ABC的面积一半,由此列出方程解答即可;
(2)分两种情况:△MCN∽△ACB,△MCN∽△BCA,得出对应线段的比计算得出答案即可.
解:(1)∵AC=8cm,BC=6cm,
∴S△ABC=24cm2,
∵CM=6﹣t,CN=3t,S△MNC=S四边形ABMN,
∴![]() ×3t(6﹣t)=12,
×3t(6﹣t)=12,
解得:t1=2,t2=4;
∵当点N到达点A时,两点都停止移动,
∴0<t<![]() ,
,
∴当t=2时,S△MNC=S四边形ABMN.
(2)①当△MCN∽△ACB时,
则![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得:t=![]() ;
;
②当△MCN∽△BCA时,
则![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得:t=![]() ,
,
答:当t为![]() 或
或![]() 时,△MNC与△ABC相似.
时,△MNC与△ABC相似.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的动点
中的动点![]() 和图形
和图形![]() ,给出如下定义:如果
,给出如下定义:如果![]() 为图形
为图形![]() 上一个动点,
上一个动点,![]() ,
,![]() 两点间距离的最大值为
两点间距离的最大值为![]() ,
,![]() ,
,![]() 两点间距离的最小值为
两点间距离的最小值为![]() ,我们把
,我们把![]() 的值叫点
的值叫点![]() 和图形
和图形![]() 间的“和距离”,记作
间的“和距离”,记作![]() (
(![]() ,图形
,图形![]() ).
).
(1)如图,正方形![]() 的中心为点
的中心为点![]() ,
,![]() .
.
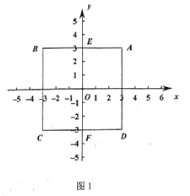
①点![]() 到线段
到线段![]() 的“和距离”
的“和距离”![]() (
(![]() ,线段
,线段![]() )=______;
)=______;
②设该正方形与![]() 轴交于点
轴交于点![]() 和
和![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() (
(![]() ,正方形
,正方形![]() )=7,求点
)=7,求点![]() 的坐标.
的坐标.
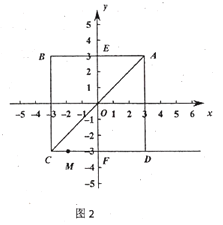
(2)如图2,在(1)的条件下,过![]() ,
,![]() 两点作射线
两点作射线![]() ,连接
,连接![]() ,点
,点![]() 是射线
是射线![]() 上的一个动点,如果
上的一个动点,如果![]() (
(![]() ,线段
,线段![]() )
)![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若P和Q两点关于原点对称,则称点P与点Q是一个“和谐点对”,表示为[P,Q],比如[P(1,2),Q(﹣1,﹣2)]是一个“和谐点对”.
(1)写出反比例函数y=![]() 图象上的一个“和谐点对”;
图象上的一个“和谐点对”;
(2)已知二次函数y=x2+mx+n,
①若此函数图象上存在一个和谐点对[A,B],其中点A的坐标为(2,4),求m,n的值;
②在①的条件下,在y轴上取一点M(0,b),当∠AMB为锐角时,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若![]() ,则
,则![]() 的值是 ___.
的值是 ___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
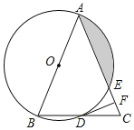
(1)求证:DF为⊙O的切线;
(2)求证:F为CE的中点;
(3)若⊙O的半径为3,∠CDF=22.5°,求阴影部分的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是⊙O的内接三角形,∠BAC的平分线交⊙O于点D.
(I)如图①,若BC是⊙O的直径,BC=4,求BD的长;
(Ⅱ)如图②,若∠ABC的平分线交AD于点E,求证:DE=DB.
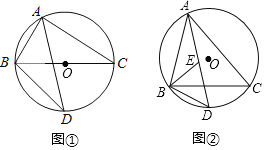
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州二中八十周年校庆来临之际,学校本着“简朴,节俭,实效,特色”的原则将 2019年 10 月 25 日至 11 月 25 日定为校友回访月,学校总务处购买了红,黄,蓝三种花卉装扮 出 A,B,C,D 四种造型,其中一个 A 造型需要 15 盆红花,10 盆黄花,10 盆蓝花;一个 B 造型需要 5 盆红花,7 盆黄花,6 盆蓝花;一个 C 造型需要 7 盆红花,8 盆黄花,9 盆蓝 花;一个 D 造型需要 7 盆红花,10 盆黄花,10 盆蓝花,若一个 A 造型售价 1800 元,利润 率为 20%,一个 B 和一个 C 造型一共成本和为 1935 元,且一盆红花的利润率为 25%,则一个 D 造型的售价为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
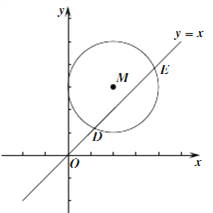
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com