
【题目】(1)证明:“三角形内角和是180°”;
(2)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据平行线的性质、平角的定义证明;
(2)根据等腰三角形的性质、三角形内角和定理证明
(1)证明:已知:△ABC, 求证:∠BAC+∠B+∠C=180°,
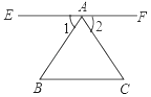
证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即知三角形内角和等于180°
(2)解:“直角三角形斜边上的中线等于斜边的一半”的逆命题是一个三角形一边上的中线是这边的一半,那么这个三角形是直角三角形,是真命题. 已知,如图,△ABC中,D是AB边的中点,且CD= ![]() AB
AB
求证:△ABC是直角三角形,
证明:∵D是AB边的中点,且CD= ![]() AB,
AB,
∴AD=BD=CD,
∵AD=CD,
∴∠ACD=∠A,
∵BD=CD,
∴∠BCD=∠B,
又∵∠ACD+∠BCD+∠A+∠B=180°,
∴2(∠ACD+∠BCD)=180°,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.



科目:初中数学 来源: 题型:
【题目】温度通常有两种表示方法:华氏度(单位:![]() )与摄氏度(单位:
)与摄氏度(单位:![]() ).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.
).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.
摄氏度数x( | … | 0 | … | 35 | … | 100 | … |
华氏度数y( | … | 32 | … | 95 | … | 212 | … |
(1)选用表格中给出的数据,求y关于x的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是![]()
![]() ,求与之对应的华氏度数.
,求与之对应的华氏度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF,
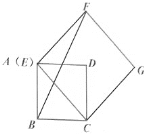
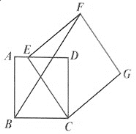
图1 图2
(1)如图1,当点E与点A重合时,则![]() _____;
_____;
(2)如图2,当点E在线段AD上时,![]() ,
,
①求点F到AD的距离;
②求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的内切圆.
(1)若∠A=60°,连接BO、CO并延长,分别交AC、AB于点D、E,
① 求∠BOC的度数;
② 试探究BE、CD、BC之间的等量关系,并证明你的结论;
(2)若AB=AC=10,sin∠ABC=![]() ,AC、AB与⊙O相切于点D、E,将BC向上平移与⊙O交于点F、G,若以D、E、F、G为顶点的四边形是矩形,求平移的距离.
,AC、AB与⊙O相切于点D、E,将BC向上平移与⊙O交于点F、G,若以D、E、F、G为顶点的四边形是矩形,求平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程是刻画现实世界的有效模型,表格是建立方程的策略之一.请填写表格数据,并列方程解决问题.轮船和汽车都从甲地开往乙地,海路比公路近40千米,轮船上午7点开出,速度是每小时24千米.汽车上午10点开出,速度为每小时40千米,结果同时到达了乙地.求甲、乙两地的海路和公路长.
速度 | 时间 | 路程 | |
汽车 | 40 |
| x |
轮船 | 24 |
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com