
【题目】如图,![]() 为等边三角形,点D、E分别在BC,AC上,AE=CD,AD交BE于点P,
为等边三角形,点D、E分别在BC,AC上,AE=CD,AD交BE于点P,![]() 于Q,
于Q,![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求AD的长.
,求AD的长.
【答案】(1)见解析;(2)7
【解析】
(1)根据等边三角形的性质,通过全等三角形的判定定理SAS证得结论;
(2)利用(1)中的全等三角形的对应角相等和三角形外角的性质求得∠BPQ=60°;求得∠PBQ=30°,所以由“30度角所对的直角边是斜边的一半”得到2PQ=BP=6,则易求BE=BP+PE=7.
(1)证明:∵△ABC为等边三角形,
∴AB=CA,∠BAE=∠C=60°,
在△AEB与△CDA中,
 ;,
;,
∴△AEB≌△CDA(SAS),
∴BE=AD;
(2)由(1)知,△AEB≌△CDA,则∠ABE=∠CAD,
∴∠BAD+∠ABE=∠BAD+∠CAD=∠BAC=60°,
∴∠BPQ=∠BAD+∠ABD=60°;
∴∠BPQ=60°.
∵BQ⊥AD,
∴∠PBQ=30°,
∴PQ=![]() BP=3,
BP=3,
∴BP=6
∴AD=BE =BP+PE=7,即AD=7.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①OG=![]() AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.其中正确的是( )
AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.其中正确的是( )
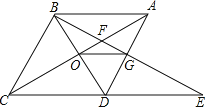
A.①④B.①③④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.

(![]() )请画出将
)请画出将![]() 向左平移
向左平移![]() 个单位长度后得到的图形
个单位长度后得到的图形![]() .
.
(![]() )请画出
)请画出![]() 关于原点
关于原点![]() 成中心对称的图形
成中心对称的图形![]()
(![]() )在
)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,请直接写出点
的值最小,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG=BE且DG⊥BE,请你给出证明.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型商业中心开业,为吸引顾客,特在一指定区域放置一批按摩休闲椅,供顾客有偿体验,收费如下图:
(1)若在此按摩椅上连续休息了1小时,需要支付多少元?
(2)某人在该椅上一次性消费18元,那么他在该椅子上最多休息了多久?
(3)张先生到该商场会见一名客人,结果客人告知临时有事,预计4.5小时后才能到来;那么如果张先生要在该休闲椅上休息直至客人到来,他至少需要支付多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形纸片ABCD中,AB=mAD,其中m1,将它沿EF折叠(点E.F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设![]() ,其中0<n1.
,其中0<n1.
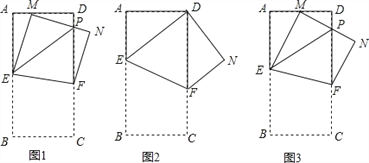
(1)如图2,当n=1(即M点与D点重合),求证:四边形BEDF为菱形;
(2)如图3,当![]() (M为AD的中点),m的值发生变化时,求证:EP=AE+DP;
(M为AD的中点),m的值发生变化时,求证:EP=AE+DP;
(3)如图1,当m=2(即AB=2AD),n的值发生变化时,![]() 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用的时间为![]() (分),所走的路程为
(分),所走的路程为![]() (米),
(米),![]() 与
与![]() 之间的函数关系如图所示,
之间的函数关系如图所示,
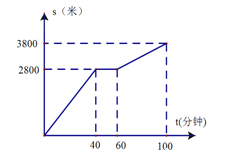
(1)小明中途休息用了_______分钟.
(2)小明在上述过程中所走的过程为________米
(3)小明休息前爬山的平均速度和休息后爬山的平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
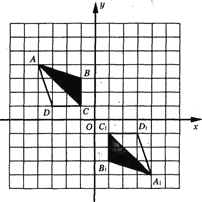
【题目】如图,在网格中、建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD 绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.
(1)直接写出点D1的坐标________,点D旋转到点D1所经过的路线长_______;
(2)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是________,则它所对应的正弦函数值是_________;
(3)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若点D2(4,5),画出平移后的图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com