
【题目】如图,在河流两边有甲、乙两座山,现在从甲山A处的位置向乙山B处拉电线,已知甲山AC的坡比为15:8.乙山BD的坡比为4:3,甲山上A点到河边c的距离AC=340米,乙山上B点到河边D的距离BD=900米,从B处看A处的俯角为26°,则河CD的宽度是(参考值:sin26°=0.4383,tan26°=0.4788,co26°=0.8988)结果精确到0.01)( )

A.177.19米B.188.85米C.192.0米D.258.25米
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】已知如图,抛物线![]() 与
与![]() 轴交于点A和点C(2,0),与
轴交于点A和点C(2,0),与![]() 轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
(1)直接写出点A和点B的坐标;
(2)求![]() 和
和![]() 的值;
的值;
(3)已知点E是该抛物线的顶点,求证:AB⊥EB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.
(1)求抛物线y=x2﹣2x+2与x轴的“和谐值”;
(2)求抛物线y=x2﹣2x+2与直线y=x﹣1的“和谐值”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
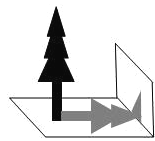
A、3.25m B、4.25m C、4.45m D、4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个正整数x的首位数字与末位数字先立方再求和得到一个新数(若x<10,则直接将x立方得到新数),定义为M(x)运算.例如:M(2)=23=8,M(31)=33+13=28,M(102)=13+23=9,规定对某个正整数x进行第一次M(x)运算记作M1(x),第二次M(x)运算记作M2(x),……,第n次M(x)运算记作Mn(x),例如:M1(2)=23=8,M2(2)=83=512,M3(2)=53+23=133.
(1)求M2(3)和M2017(3);
(2)若M5n(3)=520,求正整数n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
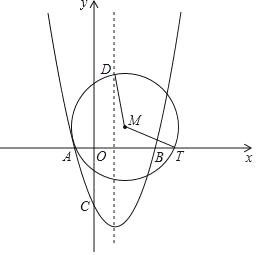
【题目】如图,二次函数y=x2+bx﹣3的图象与x轴分别相交于A、B两点,点B的坐标为(3,0),与y轴的交点为C,动点T在射线AB上运动,在抛物线的对称轴l上有一定点D,其纵坐标为2![]() ,l与x轴的交点为E,经过A、T、D三点作⊙M.
,l与x轴的交点为E,经过A、T、D三点作⊙M.
(1)求二次函数的表达式;
(2)在点T的运动过程中,
①∠DMT的度数是否为定值?若是,请求出该定值:若不是,请说明理由;
②若MT=![]() AD,求点M的坐标;
AD,求点M的坐标;
(3)当动点T在射线EB上运动时,过点M作MH⊥x轴于点H,设HT=a,当OH≤x≤OT时,求y的最大值与最小值(用含a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在△ABC中,∠ACB=90°,AC=BC过点C的射线CF交边AB于点F,AD⊥CF于点D,BE⊥CF于点E,AD=3,BE=1.
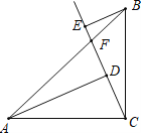
(1)求证:△ADC≌△CEB.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:平面内,如果一个四边形的四个顶点到某一点的距离都相等,则称这一点为该四边形的外心.
(1)下列四边形:平行四边形、矩形、菱形中,一定有外心的是 ;
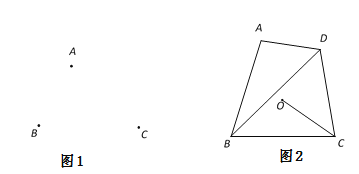
(2)已知四边形ABCD有外心O,且A,B,C三点的位置如图1所示,请用尺规确定该四边形的外心,并画出一个满足条件的四边形ABCD;
(3)如图2,已知四边形ABCD有外心O,且BC=8,sin∠BDC=![]() ,求OC的长.
,求OC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com