
ʵ����̽����
���ǵ���ǰn�еĵ�������
��ͼ��һ�����ǵ��������������������У����е�һ����1���㣬�ڶ�����2���㡭��n����n���㡭
�����֣�10�����ǵ�����ǰ4�еĵ���Լ�ͣ����ܷ���300��ǰ�����еĵ����ĺ���
���Ҫ������ķ��������϶��µ����е�������������Ȼ���ܷ���1+2+3+4+��+23+24=300����֪300��ǰ24�еĵ����ĺͣ���������Ѱ�Ҵ���������̽�����ǵ�����ǰn�еĵ����ĺ���n��������ϵ
ǰn�еĵ����ĺ���1+2+3+��+��n��2��+��n��1��+n�����Է��֣�
2��[1+2+3+��+��n��2��+��n��1��+n]
=[1+2+3+��+��n��2��+��n��1��+n]+[n+��n��1��+��n��2��+��3+2+1]
�������������еĵ�һ����ӣ��ڶ�����ӡ���n����ӣ���ʽ�Ⱥŵĺ�߱���Ϊ��n��С���Ŷ�����n+1������ʽ�ӵ���n��n+1�������ǵõ�
1+2+3+��+��n��2��+��n��1��+n= n��n+1��
n��n+1��
�����˵�����ǵ�����ǰn��ĵ����ĺ��� n��n+1��
n��n+1��
������һԪ���η��̽����������
�����ǵ�����ǰn�еĵ����ĺ�Ϊ300������ n��n+1��
n��n+1��
����������̣��ã�n2+n��600=0
�ⷽ�̵ã�n1=24��n2=25
����������δ֪��������ȷ��n=24�������ǵ�����ǰ24�еĵ����ĺ���300��
��������������ϻش��������⣺
��1�����ǵ�����ǰn�еĵ����ĺ�����600������ܣ����n��������ܣ�����һԪ���η���˵��������
��2�������ͼ�е����ǵ����и��еĵ������λ���2��4��6������2n����������̽����ǰn�еĵ����ĺ�����ʲô������������ǵ�����ǰn�еĵ����ĺ���ʹ600������ܣ����n��������ܣ�����һԪ���η���˵��������

��1��600����2��24��
��������
�����������1�������⣬�г�����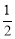 n��n+1��=600���ⷽ�̵õ�n��ֵ���ɣ�
n��n+1��=600���ⷽ�̵õ�n��ֵ���ɣ�
��2������2+4+6+��+2n=2��1+2+3+��+n��=2��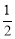 n��n+1��= n��n+1�������ݹ��ɿɵ�n��n+1��=600����n��ֵ���ɣ�
n��n+1��= n��n+1�������ݹ��ɿɵ�n��n+1��=600����n��ֵ���ɣ�
�����������������
��1��������ɵã�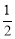 n��n+1��=600��
n��n+1��=600��
������n2+n��1200=0��
�˷������������⣬
�����ǵ�����ǰn�еĵ����ĺͲ�������600��
��2��������ɵã�2+4+6+��+2n=2��1+2+3+��+n��=2��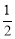 n��n+1��= n��n+1����
n��n+1��= n��n+1����
�����⣬��n��n+1��=600��
������n2+n��600=0����n+25����n��24��=0��
��n1=��25��n2=24��
��n����������n=24��
��n��ֵ��24��
���㣺1��̽�������⣨ͼ�εı仯�ࣩ��2���Ķ����������⣻3��һԪ���η��̵�Ӧ�ã�


 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ɽ��ʡ�����л��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��һ�ž���ֽƬ���ۣ��ñʼ�������������R��,����ƽ�����Կ��� �� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ɽ��ʡ�����л��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
�ⷽ�̣�
��1��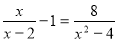 ��
��
��2��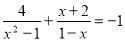 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ���ɽ������ѧ�������棩 ���ͣ�ѡ����
��ɽ�ݵ��˿�Լ��473���ˣ���473�����ÿ�ѧ��������ʾӦΪ�� ��
A��473��104�� B��4��73��106�� C��4��7��106�� D��47��3��105��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ���ɽ������ѧ�������棩 ���ͣ�ѡ����
����y=mx+n�� ������m��0��n��0����ô������ͬһ����ϵ�е�ͼ������ǣ� ��
������m��0��n��0����ô������ͬһ����ϵ�е�ͼ������ǣ� ��
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ���ɽ������ѧ�������棩 ���ͣ������
����x�ķ��� �Ľ�����������a��ȡֵ��Χ�� ��
�Ľ�����������a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㶫������ѧ�������棩 ���ͣ�ѡ����
һ������ε��ڽǺ���900�㣬�������εı����ǣ� ��
A��10 B��9 C��8 D��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㶫������ѧ�������棩 ���ͣ������
��ͼ���ڡ�ABC�У�AB=AC��AD��AB��D��BC=10cm��AD=8cm����P�ӵ�B���������߶�BC����ÿ��3cm���ٶ����C�����˶������ͬʱ����ֱ��AD��ֱ��m�ӵױ�BC��������ÿ��2cm���ٶ���DA��������ƽ�ƣ��ֱ�AB��AC��AD��E��F��H������P�����Cʱ����P��ֱ��mͬʱֹͣ�˶������˶�ʱ��Ϊt�루t��0����

��1����t=2ʱ������DE��DF����֤���ı���AEDFΪ���Σ�
��2���������˶������У����γɵġ�PEF������������ֵ������PEF��������ʱ�����߶�BP�ij���
��3���Ƿ����ijһʱ��t��ʹ��PEFΪֱ�������Σ������ڣ��������ʱ��t��ֵ���������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���˾�����ѧ�������棩 ���ͣ�ѡ����
2013��12��15�գ��ҹ������úš�����˳���ִ�������森���������ƽ��������384 400 000�ף�����384 400 000�ÿ�ѧ��������ʾΪ�� ��
A��3��844��108 B��3��844��107 C��3��844��106 D��38��44��106
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com