
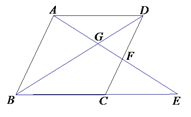
【题目】如图,在四边形ABCD中,AD//BC,E在BC的延长线,联结AE分别交BD、CD于点G、F,且![]() .
.
(1)求证:AB//CD;
(2)若![]() ,BG=GE,求证:四边形ABCD是菱形.
,BG=GE,求证:四边形ABCD是菱形.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)由AD∥BC易得![]() ,结合
,结合![]() 可得
可得![]() ,由此即可得到AB∥CD;
,由此即可得到AB∥CD;
(2)结合已知和(1)中结论易得四边形ABCD是平行四边形,由此可得BC=AD,结合BC2=GD·BD可得![]() ,结合∠ADG=∠BDA可得△ADG∽△BDA,从而可得∠DAG=∠ABD,在证∠DAG=∠E,∠E=∠DBC,∠ABD=∠BDC即可得到∠BDC=∠DBC,从而可得BC=CD结合四边形ABCD是平行四边形即可得到结论了.
,结合∠ADG=∠BDA可得△ADG∽△BDA,从而可得∠DAG=∠ABD,在证∠DAG=∠E,∠E=∠DBC,∠ABD=∠BDC即可得到∠BDC=∠DBC,从而可得BC=CD结合四边形ABCD是平行四边形即可得到结论了.
试题解析:
(1)∵AD∥BC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴AB∥CD;
(2)∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴BC=AD,
∵BC2=GD·BD,
∴AD2=GD·BD,即![]() ,
,
又∵∠ADG=∠BDA,
∴△ADG∽△BDA,
∴∠DAG=∠ABD,
∵AB∥CD,
∴∠ABD=∠BDC,
∵AD∥BC,
∴∠DAG=∠E,
∵BG=GE ,
∴∠DBC=∠E,
∴∠BDC=∠DBC,
∴BC=CD ,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形.


科目:初中数学 来源: 题型:
【题目】如图,函数![]() 的图象与函数
的图象与函数![]() 的图象交于点
的图象交于点![]() ,
,![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)观察图象,直接写出不等式![]() 的解集;
的解集;
(3)若点![]() 是
是![]() 轴上的动点,当
轴上的动点,当![]() 周长最小时,求点
周长最小时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是菱形
是菱形![]() 对角线的交点,已知菱形的边长为12,
对角线的交点,已知菱形的边长为12,![]() .
.
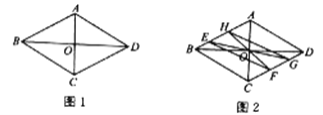
(1)求![]() 的长;
的长;
(2)如图2,点![]() 是菱形边上的动点,连结
是菱形边上的动点,连结![]() 并延长交对边于点
并延长交对边于点![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交菱形于点
交菱形于点![]() ,延长
,延长![]() 交对边于点
交对边于点![]() .
.
①求证:四边形![]() 是平行四边形;
是平行四边形;
②若动点![]() 从点
从点![]() 出发,以每秒1个单位长度沿
出发,以每秒1个单位长度沿![]() 的方向在
的方向在![]() 和
和![]() 上运动,设点
上运动,设点![]() 运动的时间为
运动的时间为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 为矩形.
为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
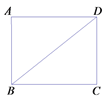
【题目】如图,在矩形ABCD中,对角线BD的长为1,点P是线段BD上的一点,联结CP,将△BCP沿着直线CP翻折,若点B落在边AD上的点E处,且EP//AB,则AB的长等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与猜想:
有一列数: 第一个数是![]() ,第二个数
,第二个数![]() ,第三个数开始依次记为
,第三个数开始依次记为![]() 、..从第二个数开始,每个数是它相邻两数和的一半.
、..从第二个数开始,每个数是它相邻两数和的一半.
(1)则第三、四、五个数分别为 、 、 ;
(2)推测![]() ______ ;
______ ;
(3)猜想第![]() 个数
个数![]() .
.
(4)计算: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
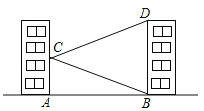
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com