
分析 根据等式的性质2:等式的两边都乘以(或除以)同一个不为零的数,结果不变,可得-$\frac{a}{b}$=-$\frac{c}{d}$,再根据等式的性质1:等式的两边都加上(或减去)同一个数,结果不变,可得答案.
解答 证明:∵$\frac{a}{b}$=$\frac{c}{d}$,
∴-$\frac{a}{b}$=-$\frac{c}{d}$,
∴1-$\frac{a}{b}$=1-$\frac{c}{d}$,
即$\frac{b-a}{b}$=$\frac{d-c}{d}$.
点评 本题考查了比例的性质,利用了等式的性质:等式的两边都乘以(或除以)同一个不为零的数,结果不变;等式的两边都加上(或减去)同一个数,结果不变.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y=-2x2 | |||||||
| y=-2x2+1 | |||||||
| y=-2x2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
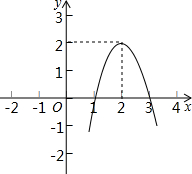 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com