
分析 (1)首先根据斜边的长和∠A的度数求得b的长,然后利用勾股定理求得a的长即可;
(2)根据直角边的长和∠B的长,然后求得另一条直角边的长,从而求得斜边的长.
解答 解:(1)∵c=6,∠A=60°,
∴$\frac{b}{c}$=cosA,
即:b=c×cosA=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{36-27}$=3;
(2)∵a=4,∠B=45°,
∴b=a=4,
c=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
故答案为:3,3$\sqrt{3}$;4,4$\sqrt{2}$.
点评 考查了解直角三角形的知识,解题的关键是能够选择合适的边角关系,难度不大.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7cm | B. | 17cm | C. | 12cm | D. | 7cm或17cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ② | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象在第一、三象限 | B. | 图象在第二、四象限 | ||
| C. | 图象在第一象限 | D. | 图象在第三象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-3,2) | C. | (3,-2) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
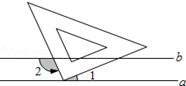 如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )
如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com