
 如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是否相似?△ACE与△BDF是否位似?试说明理由.
如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是否相似?△ACE与△BDF是否位似?试说明理由. 分析 由AC∥BD,CE∥DF,可证△OAC∽△OBD,△OCE∽△ODF,继而证得$\frac{AC}{BD}=\frac{CE}{DF}$,∠ACE=∠BDF,即可证得△ACE∽△BDF;又由△ACE与△BDF的各对应边的连线过点O,可得△ACE与△BDF位似.
解答 解:△ACE与△BDF相似,△ACE与△BDF位似.
理由:∵AC∥BD,CE∥DF,
∴△OAC∽△OBD,△OCE∽△ODF,
∴$\frac{AC}{BD}=\frac{OC}{OD}$,$\frac{OC}{OD}=\frac{CE}{DF}$,∠OCA=∠ODB,∠OCE=∠ODF,
∴$\frac{AC}{BD}=\frac{CE}{DF}$,∠ACE=∠BDF,
∴△ACE∽△BDF;
∵△ACE与△BDF的各对应顶点的连线过点O,
∴△ACE与△BDF位似.
点评 此题考查了位似变换以及相似三角形的判定与性质.注意相似三角形的各对应顶点连线过同一个点,即可得位似.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10$\sqrt{3}$cm | B. | $\frac{15}{2}$$\sqrt{3}$cm | C. | 5$\sqrt{3}$cm | D. | $\frac{5}{2}$$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
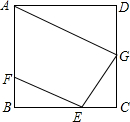 如图,正方形ABCD中,AB=1,G为DC的中点,E为BC上任意一点,(点E与B,C不重合)过E作GA的平行线交AB于F.设BE=x,四边形AFEG面积为y,试写出y关于x的函数关系式,并指出自变量x的取值范围.
如图,正方形ABCD中,AB=1,G为DC的中点,E为BC上任意一点,(点E与B,C不重合)过E作GA的平行线交AB于F.设BE=x,四边形AFEG面积为y,试写出y关于x的函数关系式,并指出自变量x的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com