
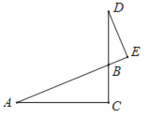
【题目】如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为________.
【答案】22.5°
【解析】
连接AD,延长AC、DE交于M,求出∠CAB=∠CDM,根据全等三角形的判定得出△ACB≌△DCM,求出AB=DM,求出AD=AM,根据等腰三角形的性质得出即可.
解: 连接AD,延长AC、DE交于M,

∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中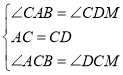
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=![]() ∠DAC=
∠DAC=![]() ×45°=22.5°,
×45°=22.5°,
故答案为:22.5°


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m2=0.
(1)求证:不论m取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求该方程的另一根。
查看答案和解析>>
科目:初中数学 来源: 题型:
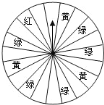
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购物满
份),并规定:顾客每购物满![]() 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得![]() 元的购物券.
元的购物券.
![]() 求转动一次转盘获得购物券的概率;
求转动一次转盘获得购物券的概率;
![]() 转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
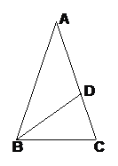
【题目】如图,已知△ABC中,D是AC边上一点,∠A=36,∠C=72,∠ADB=108。
求证:(1)AD=BD=BC;
(2)点D是线段AC的黄金分割点。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:如果
的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:如果![]() ,其中x是整数且0<y<1,那么x=1,y=
,其中x是整数且0<y<1,那么x=1,y=![]() .请解答:
.请解答:
(1)如果![]() =a+b,其中a是整数,且0<b<1,那么a= b= .
=a+b,其中a是整数,且0<b<1,那么a= b= .
(2)如果90+![]() =x+y,其中x是整数,且0<y<1,求x+
=x+y,其中x是整数,且0<y<1,求x+![]() +59-y的平方根.
+59-y的平方根.
(3)如果6+![]() 的整数部分为m,6-
的整数部分为m,6-![]() 的小数部分为n,求m-n-
的小数部分为n,求m-n-![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是____________________________________。
(2)三角形的“二分线”可以是__________________________________。
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.
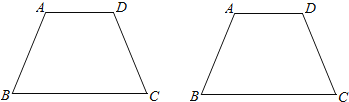
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD,BD,DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月1日起,我国将全面试行居民阶梯式电价,某市出台了实施细则,具体规定如下:
设用电量为a度,当a≤150时,电价为现行电价,每度0.51元;当150<a≤240时,在现行电价基础上,每度提高0.05元;当a>240时,在现行电价基础上,每度提高0.30元.设某户的月用电量为x(度),电费为y(元).则y与x之间的函数关系的大致图像是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com