
【题目】阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是____________________________________。
(2)三角形的“二分线”可以是__________________________________。
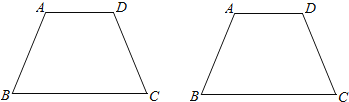
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.
【答案】菱形的一条对角线所在的直线 三角形一边中线所在的直线
【解析】
解:(1)菱形的一条对角线所在的直线。(或菱形的一组对边的中点所在的直线或菱形对角线交点的任意一条直线)。
(2)三角形一边中线所在的直线。
(3)方法一:取上、下底的中点,过两点作直线得梯形的二分线(如图1)
方法二:过A、D作AE⊥BC,DF⊥BC,垂足E、F,连接AF、DE相交于O,过点O任意作直线即为梯形的二分线(如图2)

(1)利用菱形的轴对称性
(2)三角形的中线把原三角形的面积分相等的两部分(等底同高)
(3)方法一:利用等腰梯形是轴对称图形,二分线就是它的对称轴
方法二:二分线一定过等腰梯形的对称中心


科目:初中数学 来源: 题型:
【题目】(1)已知![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,直线l经过点
,直线l经过点![]() ,分别从点
,分别从点![]() 、
、![]() 向直线l作垂线,垂足分别为
向直线l作垂线,垂足分别为![]() 、
、![]() .当点
.当点![]() ,
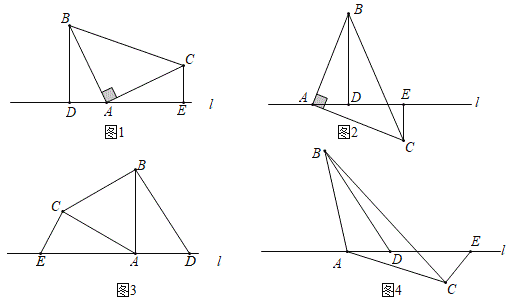
,![]() 位于直线l的同侧时(如图
位于直线l的同侧时(如图![]() ,易证
,易证![]() .如图2,若点
.如图2,若点![]() 在直线l的异侧,其它条件不变,
在直线l的异侧,其它条件不变,![]() 是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.
是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.
(2)变式一:如图3,![]() 中,
中,![]() ,直线l经过点
,直线l经过点![]() ,点
,点![]() 、
、![]() 分别在直线l上,点
分别在直线l上,点![]() 、
、![]() 位于l的同一侧,如果
位于l的同一侧,如果![]() ,求证:
,求证:![]() .
.
(3)变式二:如图4,![]() 中,依然有
中,依然有![]() ,若点
,若点![]() ,
,![]() 位于l的两侧,如果
位于l的两侧,如果![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
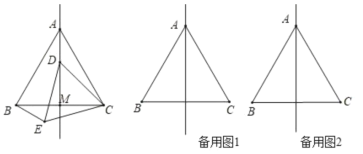
【题目】操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.

(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;
(2)在(1)的条件下,求∠BEC的度数;
拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边三角形CDE,连接BE
(1)若点D在线段AM上时,求证:△ADC≌△BEC;
(2)当动点D在直线AM上时,设直线BE与直线AM的交点为O,
①当动点D在线段AM的延长线上时,求当∠ACE为多少度时,点B、D、E在一条直线上;②当动点D在直线AM上时,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运城的桃子今年获得了大丰收,现A,B两个水果合作社要向甲,乙两个市场运送桃子,已知A可调出110吨,B可调出90吨,甲地需要80吨,乙地需要120吨,两地到甲乙市场的路程和费用如图:
路程(km) | ||
A地 | B地 | |
甲农贸市场 | 15 | 20 |
乙农贸市场 | 22 | 25 |
(1)设A地运往甲市场的桃子![]() 吨(0≤
吨(0≤![]() ≤80),则A地运往乙市场的桃子有__________吨,B地运往甲市场的桃子有___________吨,B地运往乙市场的桃子有__________吨.
≤80),则A地运往乙市场的桃子有__________吨,B地运往甲市场的桃子有___________吨,B地运往乙市场的桃子有__________吨.
(2)若每吨桃子每千米需要运费12元,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式;
(吨)的函数关系式;
(3)当A地给甲农贸市场运多少吨桃子时,总运费最省?最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
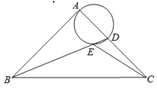
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A. 3 B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售一款李宁牌运动服,每件进价![]() 元,若按每件
元,若按每件![]() 元出售,每天可卖出
元出售,每天可卖出![]() 件,根据市场调查结果,若每件降价
件,根据市场调查结果,若每件降价![]() 元,则每天可多卖出
元,则每天可多卖出![]() 件,要使每天获得的利润最大,则每件需要降价的钱数为( )
件,要使每天获得的利润最大,则每件需要降价的钱数为( )
A. 3元 B. 4元 C. 5元 D. 8元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com