
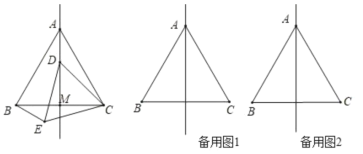
【题目】如图,在等边三角形ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边三角形CDE,连接BE
(1)若点D在线段AM上时,求证:△ADC≌△BEC;
(2)当动点D在直线AM上时,设直线BE与直线AM的交点为O,
①当动点D在线段AM的延长线上时,求当∠ACE为多少度时,点B、D、E在一条直线上;②当动点D在直线AM上时,试判断∠AOB是否为定值?并说明理由.
【答案】(1)证明见解析;(2)①150°;②是,理由见解析.
【解析】
(1)根据等边三角形的性质就可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;
(2)①根据三角形的内角和和等边三角形的性质即可得到结论;②分情况讨论,当点D在线段AM上时,由①得:∠AOB=60°;当点D在线段AM的延长线上时,证明△ACD≌△BCE(SAS),得出∠CBE=∠CAD=30°即可得出答案;当点D在线段MA的延长线上时,证明△ACD≌△BCE(SAS),得出∠CBE=∠CAD,同理得出∠CAM=30°,求出∠CBE=∠CAD=150°,得出∠CBO=30°,即可得出答案.
证明:(1)如图:
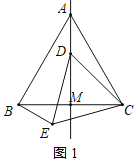
∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE,
在△ADC和△BEC中, ,
,
∴△ACD≌△BCE(SAS);
(2)解:①如图③

∵△ABC与△CDE是等边三角形,
∴∠ACB=∠DCE=60°,AC=BC,CD=CE,
∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE,
在△ACD与△BCE中, ,
,
∴△ACD≌△BCE,
又∵线段AM为BC边上的中线
∴根据等边三角形三线合一的性质可得,∠CBE=∠CAD=30°;
又∵点B、D、E在一条直线上且∠E=60°,
∴∠BCE=90°,
∴∠ACE=90°+60°=150°;
②当点D在线段AM上时,如图1所示:
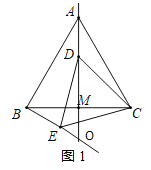
由(1)可知△ACD≌△BCE,则∠CBE=∠CAD=30°,
∵△ABC是等边三角形,线段AM为BC边上的中线
∴AM⊥BC,
∴∠BMO=90°,
∴∠AOB=90°-∠CBE=90°-30°=60°;
当点D在线段AM的延长线上时,如图2所示:
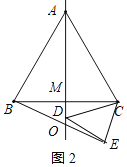
∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠DCB=∠DCB+∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中, ,
,
∴△ACD≌△BCE(SAS)
∴∠CBE=∠CAD=30°,
∴∠AOB=90°-∠CBE=90°-30°=60°;
当点D在线段MA的延长线上时,如图3所示:
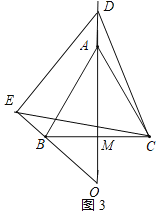
∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠ACE=∠BCE+∠ACE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中 ,
,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠CAD,
同理可得:∠CAM=30°
∴∠CBE=∠CAD=150°
∴∠CBO=30°,
∴∠AOB=90°-∠CBO=90°-30°=60°;
综上所述,当动点D在直线AM上时,∠AOB是定值,∠AOB=60°.


科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组在学习二次根式时进行了如下题目的探索研究:
(1)填空![]() ;
;![]() ;
;
(2)观察第(1)题的计算结果回答:![]() 一定等于
一定等于
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .不确定
.不确定
(3)根据(1)、(2)的计算结果进行分析总结的规律,计算:![]() .
.
(4)请你参照数学兴趣小组的研究规律,化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
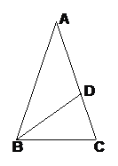
【题目】如图,已知△ABC中,D是AC边上一点,∠A=36,∠C=72,∠ADB=108。
求证:(1)AD=BD=BC;
(2)点D是线段AC的黄金分割点。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是____________________________________。
(2)三角形的“二分线”可以是__________________________________。
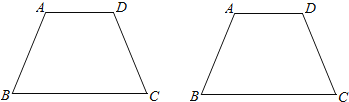
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中, 边AB的垂直平分线交对角线AC于点F,垂足为点E,连结DF,若∠BAD=80°,则∠CDF的度数为( )
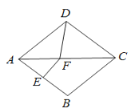
A.80°B.70°C.65°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家在甲、乙两家商场销售同一商品所获得的利润分别为![]() ,
,![]() (单位:元),
(单位:元),![]() ,
,![]() 与销售数量x(单位:件)的函数关系如图所示,试根据图象解决下列问题:
与销售数量x(单位:件)的函数关系如图所示,试根据图象解决下列问题:
(1)分别求出![]() ,
,![]() 关于x的函数关系式;
关于x的函数关系式;
(2)现厂家分配该商品800件给甲商场,400件给乙商场,当甲、乙商场售完这批商品后,厂家可获得的总利润是多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com