
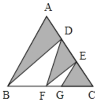
【题目】如图,AD=DE=EC,F是BC中点,G是FC中点,如果△ABC的面积是24平方厘米,则阴影部分面积是______.
【答案】14平方厘米
【解析】
连接AF,因为AD=DE=EC,所以S△ABD![]() =24×
=24×![]() =8,又因为BF=FC,所以S△ABF=S△AFC
=8,又因为BF=FC,所以S△ABF=S△AFC![]() =24×
=24×![]() =12,在△AFC中,AD=DE=EC,所以S△DEF=S△ADF=S△EFC=12×
=12,在△AFC中,AD=DE=EC,所以S△DEF=S△ADF=S△EFC=12×![]() =4,由于FG=GC,所以S△EGC=S△EFG=4×
=4,由于FG=GC,所以S△EGC=S△EFG=4×![]() =2;S阴影面积=S△ABD+S△DFE+S△GCE代入数值,进行解答即可.
=2;S阴影面积=S△ABD+S△DFE+S△GCE代入数值,进行解答即可.
解:连接AF
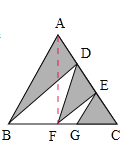
∵AD=DE=EC
∴S△ABD![]() =24×
=24×![]() =8
=8
又∵F是BC中点
∴BF=FC
∴S△ABF=S△AFC![]() =24×
=24×![]() =12
=12
∵在△AFC中,AD=DE=EC
∴S△DEF=S△ADF=S△EFC=12×![]() =4
=4
∵G是FC中点
∴FG=GC
∴S△EGC=S△EFG=4×![]() =2
=2
∴S阴影面积=S△ABD+S△DFE+S△GCE =8+4+2=14(平方厘米)
故答案为:14平方厘米.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
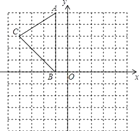
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)在y轴上找出一点P,使得PA+PB的值最小,直接写出点P的坐标;
(3)在平面直角坐标系中,找出一点A2,使△A2BC与△ABC关于直线BC对称,直接写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划安排甲乙两个施工队共同进行绿化.已知甲队每天完成绿化面积是乙队每天完成绿化面积的2倍;且甲乙两队分别完成400m2的绿化面积时,甲队比乙队少用4天.
(1)求甲、乙两队每天能完成的绿化面积分别是多少m2?
(2)学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元.已知学校计划绿化面积1800m2,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
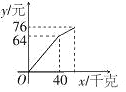
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
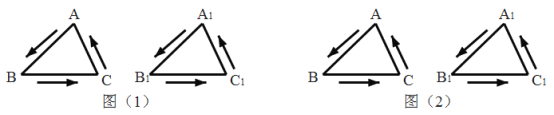
【题目】全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是合同三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1),若运动方向相反,则称它们是镜面合同三角形(如图2),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°.下列各组合同三角形中,是镜面合同三角形的是( )
A.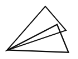 B.
B.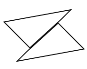 C.
C.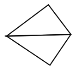 D.
D.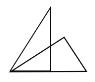
查看答案和解析>>
科目:初中数学 来源: 题型:
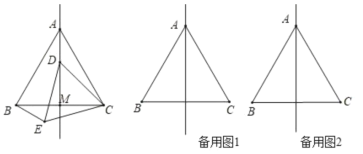
【题目】如图,在等边三角形ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边三角形CDE,连接BE
(1)若点D在线段AM上时,求证:△ADC≌△BEC;
(2)当动点D在直线AM上时,设直线BE与直线AM的交点为O,
①当动点D在线段AM的延长线上时,求当∠ACE为多少度时,点B、D、E在一条直线上;②当动点D在直线AM上时,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
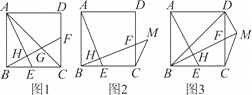
【题目】已知正方形ABCD中,点E,F分别为BC,CD上的点,连接AE,BF相交于点H,且AE⊥BF.
(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;
(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;
(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于点C,若AB=3,BC=1,则与圆环的面积最接近的整数是( )

A. 9 B. 10 C. 15 D. 13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com