
【题目】如图,四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,连接对角线
,连接对角线![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() .
.
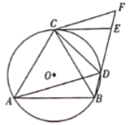
(1)求证:![]() ;
;
(2)求证:![]() .
.
【答案】(1)证明见解析;(1)证明见解析.
【解析】
(1)连接OC,由圆周角和AB=AC,易证明△ABC是正三角形,所以∠BCO=![]() ,又CE是切线,CE⊥OC,所以∠BCE=∠CBA,即可证明CE∥AB;
,又CE是切线,CE⊥OC,所以∠BCE=∠CBA,即可证明CE∥AB;
(2)因为∠BDC=![]() ,所以∠CDF=
,所以∠CDF=![]() ,又CF=DF,易证△CDF是正三角形,所以∠F=
,又CF=DF,易证△CDF是正三角形,所以∠F=![]() ,且BD+CD=BD+DF=BF,根据圆周角的性质易证∠ADC=∠ABC=∠F和∠CAB=∠CBF,又因为△ABC是正三角形,所以AC=BC,所以△ADC≌△BFC,即可得出证明AD=BD+CD.
,且BD+CD=BD+DF=BF,根据圆周角的性质易证∠ADC=∠ABC=∠F和∠CAB=∠CBF,又因为△ABC是正三角形,所以AC=BC,所以△ADC≌△BFC,即可得出证明AD=BD+CD.
证明:(1)如图,连接![]() ,
,
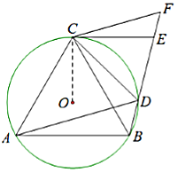
∵![]() 的内接四边形
的内接四边形![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 的切线,
的切线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆,
四点共圆,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵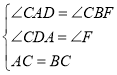 ,
,
∴![]() ,
,
∴![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市某中学“书香校园”的建设情况,在该校随机抽取了50名学生,调查了解他们一周阅读课外书籍的时间,并将调查结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值),根据图中信息估计该校1500名学生中,一周课外阅读时间不少于4小时的人数约为( )

A.300B.600C.900D.1200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)若EG平分∠HEF,求证:四边形EFGH是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
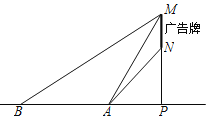
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com