
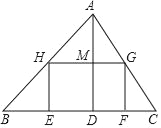
【题目】如图,△ABC的面积为12,BC与BC边上的高AD之比为3:2,矩形EFGH的边EF在BC上,点H,G分别在边AB、AC上,且HG=2GF.
(1)求AD的长;
(2)求矩形EFGH的面积.
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
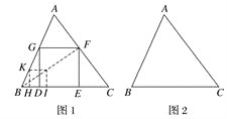
【题目】如图1,给定锐角三角形ABC,小明希望画正方形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上,他发现直接画图比较困难,于是他先画了一个正方形HIJK,使得点H,I位于射线BC上,K位于射线BA上,而不需要求J必须位于AC上.这时他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG.
阅读以上材料,回答小明接下来研究的以下问题:
(1)如图2,给定锐角三角形ABC,画出所有长宽比为2:1的长方形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上.
(2)已知三角形ABC的面积为36,BC=12,在第(1)问的条件下,求长方形DEFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,边BC长为12,高AD长为8
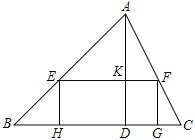
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K
①求![]() 的值
的值
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值
(2)若ABAC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线y=x2-4x+3与x轴交于点A 、B(点A在点B的左侧),与y轴交于点C.
中,抛物线y=x2-4x+3与x轴交于点A 、B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
(2)垂直于y轴的直线l与抛物线交于点![]() ,与直线BC交于点
,与直线BC交于点![]() ,若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
,若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
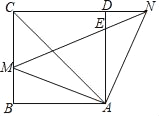
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点, ![]() ,求
,求![]() 的值;
的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证: ![]() ;
;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
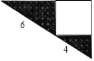
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com