
����Ŀ����ͼ1���������������ABC��С��ϣ����������DEFG��ʹD��Eλ�ڱ�BC�ϣ�F��G�ֱ�λ�ڱ�AC��AB�ϣ�������ֱ�ӻ�ͼ�Ƚ����ѣ��������Ȼ���һ��������HIJK��ʹ�õ�H��Iλ������BC�ϣ�Kλ������BA�ϣ�������Ҫ��J����λ��AC�ϣ���ʱ�����ֿ��Խ�������HIJKͨ���Ŵ����С�õ�����Ҫ���������DEFG.
�Ķ����ϲ��ϣ��ش�С���������о����������⣺
(1)��ͼ2���������������ABC���������г�����Ϊ2��1�ij�����DEFG��ʹD��Eλ�ڱ�BC�ϣ�F��G�ֱ�λ�ڱ�AC��AB�ϣ�
(2)��֪������ABC�����Ϊ36��BC��12���ڵ�(1)�ʵ������£�����DEFG�������
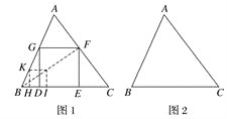
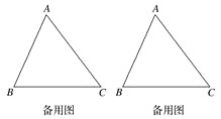
���𰸡�(1)������;(2) 18��![]() .
.
��������
��1����ͼ2���Ȼ�������HIJK��ʹ��HI=2HK������H��Iλ������BC�ϣ�Kλ������BA�ϣ�����BJ���ӳ���AC�ڵ�F���ٽ�������HIJKͨ���Ŵ�ɵõ�����Ҫ��ij�����DEFG���籸��ͼ���Ȼ�������HIJK��ʹ��HK=2HI������H��Iλ������BC�ϣ�Kλ������BA�ϣ�����BJ���ӳ���AC�ڵ�F���ٽ�������HIJKͨ���Ŵ�ɵõ�����Ҫ��ij�����DEFG��
��2������ABC�ĸ�AM����GF��N����������ABC�����Ϊ36�����AM=6������AN=x����GF��BC���ó���AGF�ס�ABC���������������ζ�Ӧ�ߵıȵ������Ʊ��г�����ʽ![]() ���ɴ����x��ֵ��������⼴�ɣ�
���ɴ����x��ֵ��������⼴�ɣ�
�⡡(1)��ͼ2�뱸��ͼ1��������DEFG��Ϊ��������ͼ�Σ�
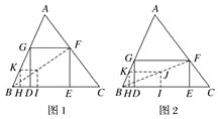
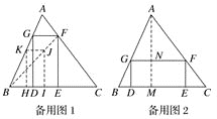
(2)�ڳ�����DEFG�У����DE��2DG���籸��ͼ2������ABC�ĸ�AM����GF��N.
��������ABC�������![]() BC��AM��
BC��AM��![]() ��12AM��36��
��12AM��36��
��AM��6.
��AN��x����MN��6��x��DG��MN��6��x��DE��GF��2(6��x)��12��2x.
��GF��BC��
���AGF�ס�ABC��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
���x��3��
��DG��6��x��3��DE��2DG��6��
�����DEFG�������6��3��18��
�ڳ�����DEFG�У����DG��2DE��ͬ�����x��![]() ��
��
��DG��6��x��![]() ��DE��
��DE��![]() DG��
DG��![]() ��
��
�����DEFG�������![]() ��
��![]() ��
��![]() .
.
�ʳ�����DEFG�����Ϊ18��![]() .
.
�ʴ�Ϊ��(1)������;(2) 18��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
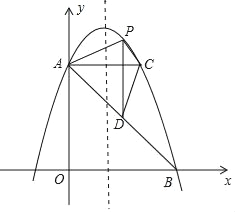
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y����x+5��y�ύ�ڵ�A����x�ύ�ڵ�B��������y����x2+bx+c��A��B���㣮
��1��д����A��B�����ꣻ
��2���������ߵĽ���ʽ��
��3������A��ACƽ����x�ᣬ���������ڵ�C����PΪ�������ϵ�һ���㣨��P��AC�Ϸ�������PDƽ����y�ύAB�ڵ�D���ʵ���P�ں�λ��ʱ���ı���APCD�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧϰ�����Ķ����н�����̣�
��һԪ���β���ʽ��x2��3x��0��
�⣺��x2��3x��0����ã�x1��0��x2��5����������y��x2��3x��x��Ľ�������Ϊ��0��0���ͣ�3��0�����������κ���y��x2��3x�Ĵ���ͼ����ͼ��ʾ������ͼ���֪����x��0��x��3ʱ����ͼ��λ��x���Ϸ�����ʱy��0����x2��3x��0�����ԣ�һԪ���β���ʽx2��3x��0�Ľ⼯Ϊ��x��0��x��3��
ͨ��������������̵�ѧϰ����������˼·�ͷ�������������⣺
��1�������������У�����������ѧ˼���е��� ������ ������ֻ����ţ�
��ת��˼�� �ڷ�������˼�� �����ν��˼�� ������˼��
��2��һԪ���β���ʽx2��3x��0�Ľ⼯Ϊ�� ����
��3�������Ƶķ�����һԪ���β���ʽ��x2��3x��4��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
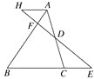
����Ŀ����ͼ����ABC�У�D��AC���е㣬E��BC�ӳ�����һ�㣬��A��AH��BE������ED���ӳ���AB��F����AH��H.
(1)��֤��AH��CE��
(2)���AB��4AF��EH��8����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
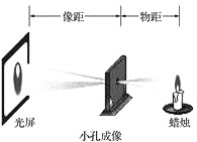
����Ŀ����ǧ����ǰ���ҹ���ѧ��ī�Ӻ�����ѧ������С�׳����ʵ�飮���������ǣ���һ��ڰ��������һ��ǽ�Ͽ�һ��С�ף�С�����ǽ�Ͼͻ�������澰��ĵ���С����ѧϰ��С�׳����ԭ����������ͼװ������֤С�׳����������֪һ����ȼ�������С��20 cm�������ھ�С��30 cm����С������������Ļ���߶�Ϊ2 cm��������ϻ���������ĸ߶�Ϊ__________ cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
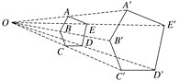
����Ŀ����ͼ����OΪλ�����ģ��������ABCDE�Ŵ�õ������A��B��C��D��E������֪OA��10 cm��OA����30 cm����S�����A��B��C��D��E����27 cm2����S�����ABCDE��__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
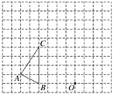
����Ŀ����ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���Ҫ����A1B1C1����A2B2C2��
(1)��OΪλ�����ģ��ڵ�O��ͬ������A1B1C1��ʹ������ԭ�����ε�λ�Ʊ�Ϊ1��2��
(2)����ABC�Ƶ�O˳ʱ����ת90���õ���A2B2C2���������A��ת��·���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϣ������Ѹ�ͷ�չ������ȥ�̳������֧����ʽ���Ӷ�������ݣ�ijУ��ѧ��ȤС�������һ�ݵ����ʾ���Ҫ��ÿ��ѡ��ֻѡһ������ϲ����֧����ʽ���ֽ�����������ͳ�Ʋ����Ƴ�����������������ͳ��ͼ������ͼ����������Ϣ����������⣺
��1����λ���������� ���ˣ�������ͳ��ͼ�У���ʾ��֧������֧��������Բ�ĽǵĶ���Ϊ�� ����
��2��������ͳ��ͼ�����������۲��ͼ��֧����ʽ���������������� ������
��3����һ�ι����У�С����С�����������������֧�������������п�������֧����ʽ��ѡһ�ַ�ʽ����֧�������û���״ͼ���б���ķ������������ǡ��ѡ��ͬһ��֧����ʽ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=ax2+bx+2��x�ύ��A��B���㣬��y�ύ�ڵ�C��AB=4������OBDC�ı�CD=1���ӳ�DC���������ڵ�E��
��1���������ߵĽ���ʽ��
��2����ͼ2����P��ֱ��EO�Ϸ��������ϵ�һ�����㣬����P��y���ƽ���߽�ֱ��EO�ڵ�G����PH��EO������ΪH����PH�ij�Ϊl����P�ĺ�����Ϊm����l��m�ĺ�����ϵʽ������д��m��ȡֵ��Χ���������l�����ֵ��
��3�������N�������߶Գ����ϵ�һ�㣬���������Ƿ���ڵ�M��ʹ����M��A��C��NΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д���������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
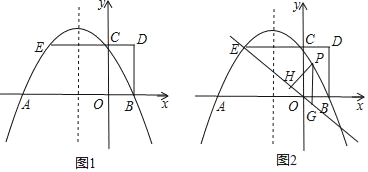
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com