【题目】小强骑自行车去郊游，右图表示他离家的距离y（千米）与所用的时间x（小时）之间关系的函数图象，小强9点离开家，15点回家，根据这个图象，请你回答下列问题：
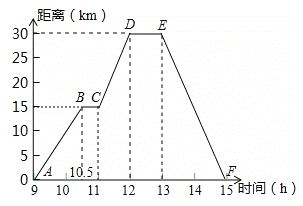
（1）小强到离家最远的地方需要几小时？此时离家多远？
（2）何时开始第一次休息？休息时间多长？
（3）小强何时距家21km？（写出计算过程）
【答案】(1)3小时,30千米;(2)10点半;半小时;(3)小强在11:24时和13:36时距家21
【解析】
（1）（2）结合图形可直接解答，由图中C，D，E，F的坐标可求CD，EF的解析式，
（3）根据距离是21，代入函数求出对应的时间
解：观察图象可知：（1）小强到离家最远的地方需要3小时，此时离家30千米；
（2）10点半时开始第一次休息；休息了半小时；
（3）点C（11，15），D（12，30），用待定系数可得DC的解析式：y=15x-150，当y=21时x=11.4，即11：24时；点E（13，30），F（15，0），用待定系数法可得EF的解析式：y=-15x+225，当y=21时x=13.6，即13：36时．
∴小强在11：24时和13：36时距家21km．
直通贵州名校周测月考直通名校系列答案科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC的两直角边AC边长为4，BC边长为3，它的内切圆为⊙O，⊙O与边AB、BC、AC分别相切于点D、E、F，延长CO交斜边AB于点G.
(1)求⊙O的半径长；
(2)求线段DG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆．
如图所示，已知：⊙I是△ABC的BC边上的旁切圆，E、F分别是切点，AD⊥IC于点D．
（1）试探究：D、E、F三点是否同在一条直线上？证明你的结论．
（2）设AB=AC=5，BC=6，如果△DIE和△AEF的面积之比等于m，
，试作出分别以
,
为两根且二次项系数为6的一个一元二次方程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，函数y=
（x＜0）的图象与直线y=
x+m相交于点A和点B．过点A作AE⊥x轴于点E，过点B作BF⊥y轴于点F，P为线段AB上的一点，连接PE、PF．若△PAE和△PBF的面积相等，且xP=﹣
，xA﹣xB=﹣3，则k的值是（ ）
A. ﹣5 B. 
C. ﹣2 D. ﹣1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=x2+2px+2p﹣2的顶点为M，
（1）求证抛物线与x轴必有两个不同交点；
（2）设抛物线与x轴的交点分别为A，B，求实数p的值使△ABM面积达到最小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=
BC，连接OE．下列结论：①∠CAD=30°；②SABCD=ABAC；③OB=AB；④OE=
BC，成立的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：小明为了计算1+2+22+……+22018+22019的值，采用以下方法：
设S=1+2+22+……+22018+22019①
则2S=2+22+……+22019+22020②
②-①得，2S-S=S=22020-1
请仿照小明的方法解决以下问题：
（1）1+2+22+……+29=；
（2）3+32+……+310=；
（3）求1+a+a2+……+an的和(a＞0，n是正整数，请写出计算过程).
查看答案和解析>>
科目：初中数学 来源： 题型：
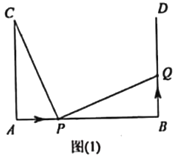
【题目】如图(1)
，
，BD⊥AB，
，点
在线段
上以
的速度由点
向点
运动，同时，点
在线段
上由点向点
运动，它们运动的时间为
.
(1)若点的速度与点的速度相等，当
时，求证：
；
(2)在(1)的条件下，判断此时
和
的位置关系，并证明；
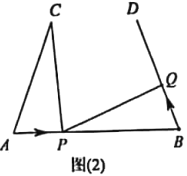
(3)将图(1)中的“，
”，改为“
”，得到图(2)，其他条件不变.设点的运动速度为
，请问是否存在实数
，使得
与
全等？若存在，求出相应的和
的值；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为保护环境，我市公交公司计划购买A型和B型两种环保节能公交车共10辆．若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
（1）求购买A型和B型公交车每辆各需多少万元？
（2）预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？
（3）在（2）的条件下，哪种购车方案总费用最少？最少总费用是多少万元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com