
【题目】如图,Rt△ABC的两直角边AC边长为4,BC边长为3,它的内切圆为⊙O,⊙O与边AB、BC、AC分别相切于点D、E、F,延长CO交斜边AB于点G.
(1)求⊙O的半径长;
(2)求线段DG的长.

【答案】(1) 1;(2)![]()
【解析】
(1)由勾股定理求AB,设⊙O的半径为r,则r=![]() (AC+BC-AB)求解;
(AC+BC-AB)求解;
(2)过G作GP⊥AC,垂足为P,根据CG平分直角∠ACB可知△PCG为等腰直角三角形,设PG=PC=x,则CG=![]() x,由(1)可知CO=
x,由(1)可知CO=![]() r=
r=![]() ,由Rt△AGP∽Rt△ABC,利用相似比求x,由OG=CG-CO求OG,在Rt△ODG中,由勾股定理求DG.
,由Rt△AGP∽Rt△ABC,利用相似比求x,由OG=CG-CO求OG,在Rt△ODG中,由勾股定理求DG.
试题解析:(1)在Rt△ABC中,由勾股定理得AB=![]() =5,
=5,
∴☉O的半径r=![]() (AC+BC-AB)=
(AC+BC-AB)=![]() (4+3-5)=1;
(4+3-5)=1;
(2)过G作GP⊥AC,垂足为P,设GP=x,
由∠ACB=90°,CG平分∠ACB,得∠GCP=45°,
∴GP=PC=x,
∵Rt△AGP∽Rt△ABC,
∴![]() =
=![]() ,解得x=
,解得x=![]() ,
,
即GP=![]() ,CG=
,CG=![]() ,
,
∴OG=CG-CO=![]() -
-![]() =
=![]() ,
,
在Rt△ODG中,DG=![]() =
=![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字![]() ,另一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字
,另一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字![]() (如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一个人口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一个人口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
⑴.用树状图或列表法求出小颖参加比赛的概率;
⑵.你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏的规则,使游戏公平.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边的中线,∠ADC=30°,将△ADC沿AD折叠,使C点落在C′的位置,若BC=4,则BC′的长为 ( )

A. 2![]() B. 2 C. 4 D. 3
B. 2 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(0,a),B(b,0)且a、b满足|a+2b﹣6|+|a﹣2b+2|=0.E为线段AB上一动点,∠BED=![]() ∠OAB,BD⊥EC,垂足在EC的延长线上,试求:
∠OAB,BD⊥EC,垂足在EC的延长线上,试求:

(1)判断△OAB的形状,并说明理由;
(2)如图1,当点E与点A重合时,探究线段AC与BD的数量关系,并证明你的结论;
(3)如图2,当点E在线段AB(不与A、B重合)上运动时,试探究线段EC与BD的数量关系,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红驾车从甲地到乙地,她出发第xh时距离乙地ykm,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
(1)B点的坐标为( , );
(2)求线段AB所表示的y与x之间的函数表达式;
(3)小红休息结束后,以60km/h的速度行驶,则点D表示的实际意义是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,过顶点
,过顶点![]() 作射线
作射线![]() .
.
(1)当射线![]() 在
在![]() 外部时,如图①,点
外部时,如图①,点![]() 在射线
在射线![]() 上,连结
上,连结![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,
,![]() (
(![]() ).
).
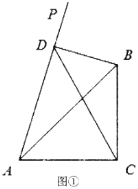
①试证明![]() 是直角三角形;
是直角三角形;
②求线段![]() 的长.(用含
的长.(用含![]() 的代数式表示)
的代数式表示)
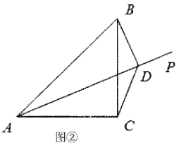
(2)当射线![]() 在
在![]() 内部时,如图②,过点
内部时,如图②,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,请写出线段
,请写出线段![]() 、
、![]() 、
、![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强骑自行车去郊游,右图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小强9点离开家,15点回家,根据这个图象,请你回答下列问题:
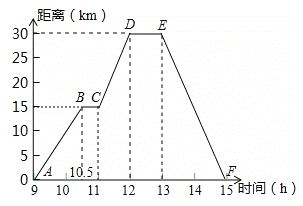
(1)小强到离家最远的地方需要几小时?此时离家多远?
(2)何时开始第一次休息?休息时间多长?
(3)小强何时距家21km?(写出计算过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com