
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�A��0��a����B��b��0����a��b����|a+2b��6|+|a��2b+2|��0��EΪ�߶�AB��һ���㣬��BED��![]() ��OAB��BD��EC��������EC���ӳ����ϣ�����
��OAB��BD��EC��������EC���ӳ����ϣ�����

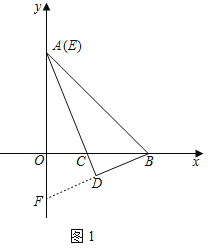
��1���жϡ�OAB����״����˵�����ɣ�
��2����ͼ1������E���A�غ�ʱ��̽���߶�AC��BD��������ϵ����֤����Ľ��ۣ�
��3����ͼ2������E���߶�AB������A��B�غϣ����˶�ʱ����̽���߶�EC��BD��������ϵ��֤����Ľ��ۣ�
���𰸡���1����OAB�ǵ���ֱ�������Σ���2��AC��2BD�����ɼ���������3��EC��2BD��֤��������
��������
��1�����ݷǸ��Եó�a��b��ֵ������ɣ�
��2���ӳ�BD��y�ύ�ڵ�F��֤����ABD�ա�AFD���ɵ�BD��DF����֤����AOC�ա�BOF���ɵ�AC��BF�����ɵó����ۣ�
��3������E��EN��x���ڵ�K����BD���ӳ����ڵ�N��֤����EBD�ա�END���ɵ�BD��DN����֤����EKC�ա�BKN���ɵ�EC��BN������۵�֤��
�⣺��1����|a+2b��6|+|a��2b+2|��0��|a+2b��6|��0��|a��2b+2|��0
��![]() ��
��
���![]() ��
��
��OA��OB��
�֡ߡ�AOB��90����
���OAB�ǵ���ֱ�������Σ�
��2��AC��2BD���������£���ͼ1���ӳ�BD��y�ύ�ڵ�F��
��![]() ��
��
���BAD����FAD
�֡�BD��EC����ADB����ADF��
�ڡ�ADB�͡�ADF�У�
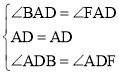 ��
��
���ABD�ա�AFD��ASA����
��BD��DF��
��![]()
��![]()
�ڡ�AOC�͡�BOF��
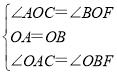
���AOC�ա�BOF��ASA����
��AC��BF��
��AC��2BD��
��3��EC��2BD��֤�����£�
��ͼ2������E��EN��x���ڵ�K����BD���ӳ����ڵ�N��
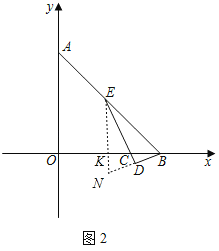
��EN��y��
���NEB����OAB��
�ߡ�BED��![]() ��OAB��
��OAB��
���NED����BED��
�ڡ�EBD�͡�END�У�
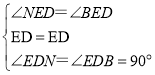 ��
��
���EBD�ա�END��ASA����
��BD��DN��
![]()
��![]()
�ڡ�EKC�͡�BKN�У�
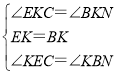
���EKC�ա�BKN��ASA����
��EC��BN��
��EC��2BD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У���D���߶�AB�ϣ���E��CD���ӳ����ϣ�����AE��AE=AC��AFƽ����EAB����CE�ڵ�F������BF.
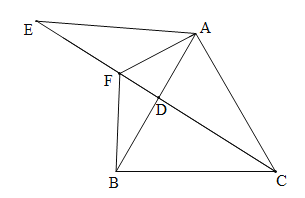
��1����֤��EF=BF��
��2��������AFC�Ķ�������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪������y=��![]() x2+
x2+![]() x+
x+![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����D�ǵ�C���������߶Գ���ĶԳƵ㣬����CD������D��DH��x���ڵ�H������A��AE��AC��DH���ӳ����ڵ�E��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����D�ǵ�C���������߶Գ���ĶԳƵ㣬����CD������D��DH��x���ڵ�H������A��AE��AC��DH���ӳ����ڵ�E��
��1�����߶�DE�ij��ȣ�
��2����ͼ2�������߶�AE����һ��F�����߶�DE����һ��P���ҵ�MΪֱ��PF�Ϸ��������ϵ�һ�㣬����CPF���ܳ���Сʱ����MPF��������ֵ�Ƕ��٣�
��3���ڣ�2���ʵ������£����õ�����CFP��ֱ��AEƽ�Ƶõ���C��F��P��������C��F��P����C��P�����۵õ���C��P��F��������ƽ�ƹ����У�ֱ��F��P����x�ύ�ڵ�K�����Ƿ���������ĵ�K��ʹ����F��F��KΪ���������Σ����������OK��ֵ���������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ������A��B������ֱ�ΪA��1��0����B��3��0����̽����������![]() ��mΪ��������x���ڵ�M��N������
��mΪ��������x���ڵ�M��N������
��1����m��2ʱ��
����������ߵĶ������꼰�߶�MN�ij���
������������һ��P��ʹ![]() �������P��������
�������P��������
��2������������![]() ��m��������
��m��������
���߶�MN�ij��Ƿ����仯����˵��������
���������������߶�AB�й���������ֱ��д��m��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC����ֱ�DZ�AC�߳�Ϊ4��BC�߳�Ϊ3����������ԲΪ��O����O���AB��BC��AC�ֱ������ڵ�D��E��F���ӳ�CO��б��AB�ڵ�G.
(1)���O�İ뾶����
(2)���߶�DG�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������12����������y=-x2+��m-1��x+m��y�ύ����0��3���㣮

��1�����m��ֵ���������������ߣ�
��2��������x��Ľ���������߶�������ꣻ
��3��xȡʲôֵʱ����������x���Ϸ���
��4��xȡʲôֵʱ��y��ֵ��xֵ���������С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ֱ��������ABC�У���BAC=90�㣬AB=AC��DΪBC���е㣬EΪAC��һ�㣬��G��BE�ϣ�����DG���ӳ���AE��F������FGE=45�㣮

��1����֤��BDBC=BGBE��
��2����֤��AG��BE��
��3����EΪAC���е㣬��EF��FD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x��8��x�ᣬy��ֱ��ڵ�A��B��ֱ��y��x��1��ֱ��AB���ڵ�C����y�ύ�ڵ�D��
x��8��x�ᣬy��ֱ��ڵ�A��B��ֱ��y��x��1��ֱ��AB���ڵ�C����y�ύ�ڵ�D��

��1�����C�����꣮
��2������BDC�������
��3����ͼ��P��y���������ϵ�һ�㣬Q��ֱ��AB�ϵ�һ�㣬����PQ��

����PQ��x�ᣬ�ҵ�A����ֱ��PQ�ĶԳƵ�A��ǡ������ֱ��CD�ϣ���PQ�ij���
������BDC����BPQȫ��(��Q�����C�غ�)����д����������Ҫ��ĵ�Q����(ֱ��д����).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���AC��BD���ڵ�O��AEƽ����BAD��BC�ڵ�E������ADC=60�㣬AB=![]() BC������OE�����н��ۣ��١�CAD=30�㣻��SABCD=ABAC����OB=AB����OE=
BC������OE�����н��ۣ��١�CAD=30�㣻��SABCD=ABAC����OB=AB����OE=![]() BC�������ĸ����У�������
BC�������ĸ����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com