
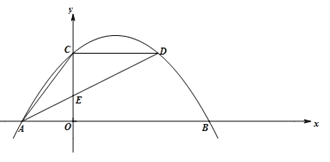
【题目】如图,已知抛物线![]() 经过A(-3,0)、B(8,0)、C(0,4)三点,点D是抛物线上的动点,连结AD与y轴相交于点E,连结AC,CD.
经过A(-3,0)、B(8,0)、C(0,4)三点,点D是抛物线上的动点,连结AD与y轴相交于点E,连结AC,CD.
(1)求抛物线所对应的函数表达式;
(2)当AD平分∠CAB时.
①求直线AD所对应的函数表达式;
②设P是x轴上的一个动点,若△PAD与△CAD相似,求点P的坐标.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②(2,0)或(13,0).
;②(2,0)或(13,0).
【解析】
(1)将![]() 、
、![]() 、
、![]() 点坐标代入抛物线
点坐标代入抛物线![]() ,化简计算即可;
,化简计算即可;
(2)![]() 设
设![]() ,根据
,根据![]() 平分
平分![]() ,
,![]() ,
,![]() 轴,求得
轴,求得![]() ,并证得
,并证得![]() ∽
∽ ![]() ,利用
,利用![]() 可的
可的![]() ,可得
,可得![]() 点坐标,把
点坐标,把![]() ,
,![]() 代入
代入![]() ,化简可得AD所对应的函数表达式;
,化简可得AD所对应的函数表达式;
![]() 因为
因为![]() 是x轴上的一个动点,且
是x轴上的一个动点,且![]() 与
与![]() 相似,并且
相似,并且![]() 是腰长为5的等腰三角形,所以
是腰长为5的等腰三角形,所以 ![]() 点有两种情况:AD为等腰三角形的斜边,或者以AD为腰,
点有两种情况:AD为等腰三角形的斜边,或者以AD为腰,![]() 为底,分别讨论求解即可.
为底,分别讨论求解即可.
解(1)∵抛物线经过![]() 、
、![]() 、
、![]() 三点,
三点,
∴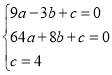 ,解得:
,解得: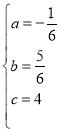 ,
,
∴抛物线的表达式为![]() ;
;
(2)![]() 作
作![]() 于点H,如图,设
于点H,如图,设![]() .
.
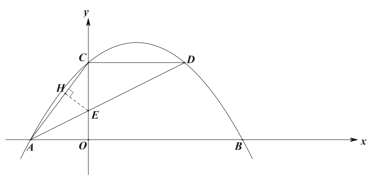
∵![]() 平分
平分![]() ,
,![]() ,
,![]() 轴,
轴,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.
∵![]()
![]() ,
,
∴![]() ∽
∽ ![]() ,
,
∴![]()
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ,设直线AD的表达式为
,设直线AD的表达式为![]() ,
,
把![]() ,
,![]() 代入,
代入,
得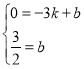 ,解得:
,解得:![]() ,
,
∴直线AD所对应的函数表达式为![]() ;
;
![]() 直线AD与二次函数相交于点D,
直线AD与二次函数相交于点D,
∴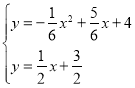 解得
解得![]() 或
或![]() ,
,
![]() 点D在第一象限,
点D在第一象限,
∴点D坐标为![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() 是腰长为5的等腰三角形,
是腰长为5的等腰三角形,
![]() 是x轴上的一个动点,且
是x轴上的一个动点,且![]() 与
与![]() 相似,
相似,
∴![]() 也为等腰三角形,
也为等腰三角形,
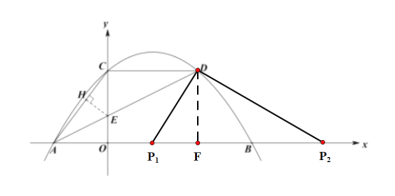
如上图示,
当AD为等腰三角形的斜边时,![]() ,
,
![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
当以AD为腰,![]() 为底时,作
为底时,作![]()
![]() 点D坐标为
点D坐标为![]() ,
,![]()
∴![]()
∴![]() ,
,![]() ,
,
∴点P的坐标为![]() .
.
综上所述点P的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A、B的坐标分别为(﹣1,1)、(3,0),直角顶点C在x轴上,在△ADE中,∠E=90°,点D在第三象限的双曲线y=![]() 上,且边AE经过点C.若AB=AD,∠BAD=90°,则k的值为( )
上,且边AE经过点C.若AB=AD,∠BAD=90°,则k的值为( )
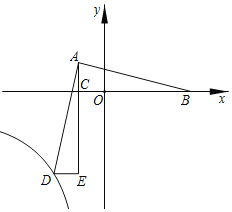
A.3B.4C.﹣6D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
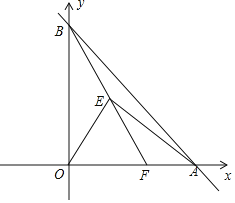
【题目】如图,在直角坐标系中,直线![]() 与x轴正半轴,y轴正半轴分别交于点A,B,点
与x轴正半轴,y轴正半轴分别交于点A,B,点![]() ,点E在第一象限,
,点E在第一象限,![]() 为等边三角形,连接AE,BE
为等边三角形,连接AE,BE
![]() 求点E的坐标;
求点E的坐标;
![]() 当BE所在的直线将
当BE所在的直线将![]() 的面积分为3:1时,求
的面积分为3:1时,求![]() 的面积;
的面积;
![]() 取线段AB的中点P,连接PE,OP,当
取线段AB的中点P,连接PE,OP,当![]() 是以OE为腰的等腰三角形时,则
是以OE为腰的等腰三角形时,则![]() ______
______![]() 直接写出b的值
直接写出b的值![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
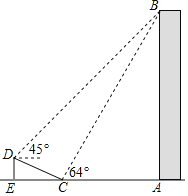
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)我市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
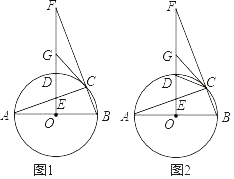
【题目】如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BCBF;
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为( )
上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为( )
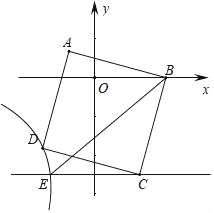
A. 5B. 6C. 7D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com