【题目】日历上的规律：表格是2020年元月的日历，图中的阴影区域是在日历中选取的一块九宫格.
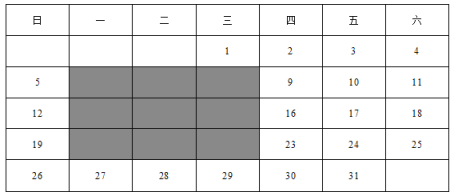
（1）九宫格中，四个角的四个数之和与九宫格中央那个数有什么关系？
（2）请你自选一块九宫格进行计算，看四个角上的四个数之和与九宫格中央那个数是否还有这种关系？
（3）试说明原理.
【答案】（1）四个角上的四个数之和等于九宫格中央这个数的4倍；（2）有；（3）详见解析.
【解析】
（1）先分别找出四个角的四个数与九宫格中央所代表的数，然后通过计算即可得出结论；
（2）根据上图随意找出九个数然后计算，观察是否符合结论；
（3）设九宫格中央这个数为
，那么上角两个数分别为
、
，下角两个数分别为
、
，然后通过计算验证即可.
解：（1）根据题意可知四个角的四个数与九宫格中央所代表的数分别为：6,22,8,20与14
则
.
即四个角上的四个数之和等于九宫格中央这个数的4倍；
（2）取如下图的数据
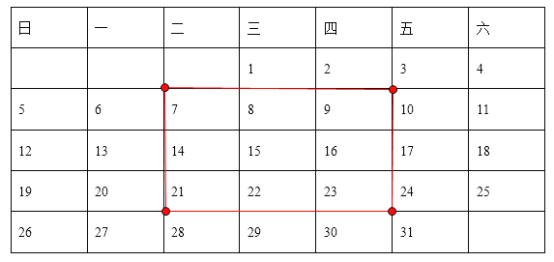
则有
即四个角上的四个数之和等于九宫格中央这个数的4倍；
（3）设九宫格中央这个数为，那么上角两个数分别为、，
下角两个数分别为、，
四个数的和：
.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，一次函数
（k≠0）的图象与反比例函数
（m≠0，x＜0）的图象交于点A（-3，1）和点C，与y轴交于点B，△AOB的面积是6．
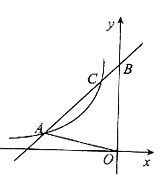
（1）求一次函数与反比例函数的解析式；
（2）求 sin∠ABO的值；
（3）当x＜0时，比较
与
的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若二次函数y=ax2+bx﹣4的图象开口向上，与x轴的交点为（4，0）、（﹣2，0），则当x1=﹣1，x2=2时，对应的函数值y1和y2的大小关系为（ ）
A. y1＞y2 B. y1=y2 C. y1＜y2 D. 不确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，若△CEF的面积为18cm2，则S△DGF等于（ ）
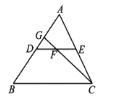
A.4cm2B.5cm2C.6cm2D.7 cm2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分ABC，P是BD上一点，过点P作PM^AD，PN^CD，垂足分别为M、N。
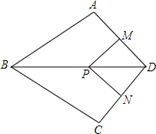
（1）求证：ADB=CDB；
（2）若ADC=90°，求证：四边形MPND是正方形。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PB＝PE，连接PD，O为AC中点．
(1)如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，不用说明理由；
(2)如图2，当点P在线段OC上时，(1)中的猜想还成立吗？请说明理由；
(3)如图3，当点P在AC的延长线上时，请你在图3中画出相应的图形(尺规作图，保留作图痕迹，不写作法)，并判断(1)中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于三角函数有如下的公式：
sin（α+β）=sinαcosβ+cosαsinβ①
cos（α+β）=cosαcosβ﹣sinαsinβ②
tan（α+β）=
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值，如：
tan105°=tan（45°+60°）=
=﹣（2+
）．
根据上面的知识，你可以选择适当的公式解决下面的实际问题：
如图，直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°，底端C点的俯角β=75°，此时直升飞机与建筑物CD的水平距离BC为42m，求建筑物CD的高．
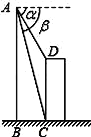
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AC，BD相交于点O，O是AC的中点，AD//BC，AC=8,BD=6.
（1）求证：四边形ABCD是平行四边形；
（2）若AC⊥BD，求□ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
