
����Ŀ����ͼ����P��������ABCD�Խ���AC��һ���㣬��E������BC�ϣ���PB��PE������PD��OΪAC�е㣮
(1)��ͼ1������P���߶�AO��ʱ���Բ���PE��PD��������ϵ��λ�ù�ϵ������˵�����ɣ�
(2)��ͼ2������P���߶�OC��ʱ��(1)�еIJ��뻹��������˵�����ɣ�
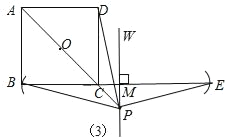
(3)��ͼ3������P��AC���ӳ�����ʱ��������ͼ3�л�����Ӧ��ͼ��(�߹���ͼ��������ͼ�ۼ�����д����)�����ж�(1)�еIJ����Ƿ����������������ֱ��д�����ۣ�������������˵�����ɣ�

���𰸡�(1)PE��PD��������ϵ��λ�ù�ϵ�ֱ�Ϊ��PE��PD��PE��PD��(2)���������ɼ�������(3)���������ɼ�����.
��������
��1�����ݵ�P���߶�AO��ʱ�����������ε�ȫ���ж����Եó�PE��PD��PE��PD��
��2������������ȫ�ȵó���BP��PD����PB��PE���ó�PE��PD��Ҫ֤PE��PD�������������������E���߶�BC�ϣ�E��B��C���غϣ�ʱ������E���C�غ�ʱ����Pǡ����AC�е㴦������E��BC���ӳ�����ʱ���ֱ�������ɵó���
��3������PE��PB�ó�P����BE�Ĵ�ֱƽ�����ϣ����ô�ֱƽ���ߵ�����ֻҪ��PΪԲ�ģ�PBΪ�뾶�������ɵó�E��λ�ã����ã�2����֤��˼·���ɵó��𰸣�
(1)����P���߶�AO��ʱ��
����ABP����ADP�� ��
��
���ABP�ա�ADP��
��BP��DP��
��PB��PE��
��PE��PD��
����P��PM��CD�ڵ�M����PN��BC���ڵ�N��
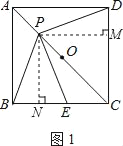
��PB��PE��PN��BE��
��BN��NE��
��BN��DM��
��DM��NE��
��Rt��PNE��Rt��PMD��
��PD��PE��NE��DM��
��Rt��PNE��Rt��PMD��
���DPM����EPN��
�ߡ�MPN��90����
���DPE��90����
��PE��PD��
PE��PD��������ϵ��λ�ù�ϵ�ֱ�Ϊ��PE��PD��PE��PD��
(2)���ı���ABCD�������Σ�ACΪ�Խ��ߣ�
��BA��DA����BAP����DAP��45����
��PA��PA��
���BAP�ա�DAP(SAS)��
��PB��PD��
�֡�PB��PE��
��PE��PD��
(i)����E���C�غ�ʱ����Pǡ����AC�е㴦����ʱ��PE��PD��
(ii)����E��BC���ӳ�����ʱ����ͼ��
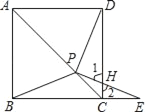
�ߡ�ADP�ա�ABP��
���ABP����ADP��
���CDP����CBP��
��BP��PE��
���CBP����PEC��
���PEC����PDC��
�ߡ�1����2��
���DPE����DCE��90����
��PE��PD��
�ۺ�(i)(ii)��PE��PD��
(3)ͬ�����ɵó���PE��PD��PD��PE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
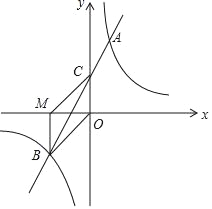
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=mx+n��m��0����ͼ���뷴��������y=![]() ��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2
��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2![]() ����A��������Ϊ4��
����A��������Ϊ4��
��1����÷�����������һ�κ����Ľ���ʽ��
��2������MC�����ı���MBOC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
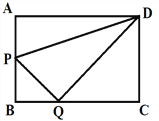
����Ŀ���ھ���ABCD�У�AB=3��AD=4������P�ӵ�B��������ÿ��1����λ���ٶȣ���BA���A�ƶ���ͬʱ��Q�ӵ�C��������ÿ��2����λ���ٶȣ���CB���B�ƶ�������QP��QD��PD����������ͬʱ�˶���ʱ��Ϊx�루0<x��2��������������⣺
��1����xΪ��ֵʱ��PQ��DQ��
��2������QPD�����ΪS���ú�x�ĺ�����ϵʽ��ʾS����xΪ��ֵʱ��S����Сֵ���������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵĹ��ɣ�������2020��Ԫ�µ�������ͼ�е���Ӱ��������������ѡȡ��һ��Ź���.
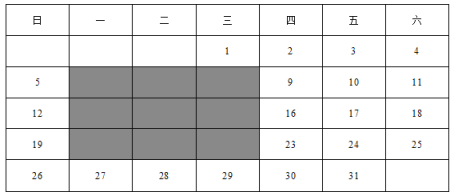
��1���Ź����У��ĸ��ǵ��ĸ���֮����Ź��������Ǹ�����ʲô��ϵ��
��2��������ѡһ��Ź�����м��㣬���ĸ����ϵ��ĸ���֮����Ź��������Ǹ����Ƿ������ֹ�ϵ��
��3����˵��ԭ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
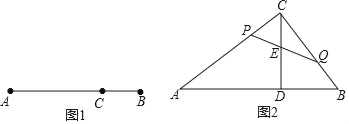
����Ŀ�����壺����C���߶�AB�ϣ�AC=nABʱ�����dz�nΪ��C���߶�AB�ϵĵ�ֵ������dC��AB=n�����C��AB���е�ʱ����AC=![]() AB����dC��AB=
AB����dC��AB=![]() ������������dC��AB=
������������dC��AB=![]() ʱ������AC=
ʱ������AC=![]() AB��
AB��
��1����ͼ1����C���߶�AB�ϣ���dC��AB=![]() ����
����![]() =�� ������AC=3BC����dC��AB=�� ����
=�� ������AC=3BC����dC��AB=�� ����
��2����ͼ2������ABC�У���ACB=90�㣬CD��AB�ڵ�D��AB=10cm��BC=6cm����P��Q�ֱ�ӵ�C�͵�Bͬʱ��������P���߶�CA��2cm/s���ٶ����A�˶�����Q���߶�BC��1cm/s���ٶ����C�˶�������P�����Aʱ����P��Q��ֹͣ�˶�������PQ��CD�ڵ�E�����˶�ʱ��Ϊts��dP��CA+dQ��CB=m��
�ٵ�![]() ��m��
��m��![]() ʱ����t��ȡֵ��Χ��
ʱ����t��ȡֵ��Χ��
�ڵ�dP��CA=![]() ����dE��CD��ֵ��
����dE��CD��ֵ��
�۵�dE��CD=![]() ʱ����t��ֵ��
ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�IJ���ʽ![]() ��
��![]() x��1��
x��1��
��1����m=1ʱ����ò���ʽ�Ľ⼯��
��2��mȡ��ֵʱ���ò���ʽ�н⣬������⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͯ����߳����˵Ĺ���ʱ��Ϊ��ÿ��22�죬ÿ��8Сʱ�����ʴ���Ϊ�������Ƴ꣬���Ͷ�ã�ÿ�����Ӹ�������500Ԫ�����½��㣮�ó�����A��B���ֲ�Ʒ������ÿ����һ��A�ֲ�Ʒ�ɵñ���1.50Ԫ��ÿ����һ��B�ֲ�Ʒ�ɵñ���2.80Ԫ���ó����˿���ѡ��A��B���ֲ�Ʒ�е�һ�ֻ����ֽ�������������С������1��A��Ʒ��1��B��Ʒ��35���ӣ�����3��A��Ʒ��2��B��Ʒ��85���ӣ�
��1��С������1��A��Ʒ��Ҫ�� �����ӣ�����1��B��Ʒ��Ҫ�� �����ӣ�
��2����С��ÿ�µĹ������뷶Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������е�ÿ��С�����εı߳�����1��ÿ��С��Ķ��������㣮
��1����ͼ1���Ը��Ϊ���㻭һ�����Ϊ10�������Σ�
��2����ͼ2���Ը��Ϊ���㻭һ�������Σ�ʹ���������߳��ֱ�Ϊ2��![]() ��
��![]() ��
��
��3����ͼ3����A��B��C��С�����εĶ��㣬���ABC�Ķ�����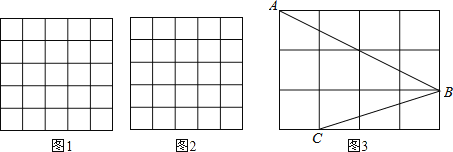
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB=AC��

��1������ֱ�ߺ�Բ����AC����һ��D��ʹAD=BD����д���������豣����ͼ�ۼ�����
��2���ڣ�1���У�����BD����BD=BC�����A�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com