
【题目】定义:当点C在线段AB上,AC=nAB时,我们称n为点C在线段AB上的点值,记作dC﹣AB=n.如点C是AB的中点时,即AC=![]() AB,则dC﹣AB=
AB,则dC﹣AB=![]() ;反过来,当dC﹣AB=
;反过来,当dC﹣AB=![]() 时,则有AC=
时,则有AC=![]() AB.
AB.
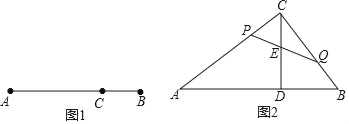
(1)如图1,点C在线段AB上,若dC﹣AB=![]() ,则
,则![]() = ;若AC=3BC,则dC﹣AB= ;
= ;若AC=3BC,则dC﹣AB= ;
(2)如图2,在△ABC中,∠ACB=90°,CD⊥AB于点D,AB=10cm,BC=6cm,点P、Q分别从点C和点B同时出发,点P沿线段CA以2cm/s的速度向点A运动,点Q沿线段BC以1cm/s的速度向点C运动,当点P到达点A时,点P、Q均停止运动,连接PQ交CD于点E,设运动时间为ts,dP﹣CA+dQ﹣CB=m.
①当![]() ≤m≤
≤m≤![]() 时,求t的取值范围;
时,求t的取值范围;
②当dP﹣CA=![]() ,求dE﹣CD的值;
,求dE﹣CD的值;
③当dE﹣CD=![]() 时,求t的值.
时,求t的值.
【答案】(1)![]() ,
,![]() ;(2)①3≤t≤4;②0.6;③t的值为2.4或
;(2)①3≤t≤4;②0.6;③t的值为2.4或![]()
【解析】分析:(1)当点C在线段AB上,AC=nAB时,我们称n为点C在线段AB上的点值,记作dC-AB=n,据此进行判断即可;
(2)①根据dP-CA=![]() ,dQ-CB=
,dQ-CB=![]() ,即可得到m=dP-CA+dQ-CB=
,即可得到m=dP-CA+dQ-CB=![]() ,再根据
,再根据![]() ,即可得到不等式
,即可得到不等式![]() ,进而解得3≤t≤4;
,进而解得3≤t≤4;
②根据dP-CA=![]() ,dP-CA+dQ-CB=m,可得dP-CA=dQ-CB,即
,dP-CA+dQ-CB=m,可得dP-CA=dQ-CB,即![]() ,进而得出
,进而得出![]() ,求得t=2.4,再根据
,求得t=2.4,再根据![]() ,∠ACB=∠PCQ,判定△ACB∽△PCQ,进而得到PQ∥AB,得出
,∠ACB=∠PCQ,判定△ACB∽△PCQ,进而得到PQ∥AB,得出![]() ,即可得到dE-CD=dP-CA=
,即可得到dE-CD=dP-CA=![]() =0.6;
=0.6;
③分两种情况:当PQ∥AB时,则有dE-CD=dP-CA=dQ-CB=![]() ,由②可得,t=2.4;当PQ与AB不平行时,过点P,Q分别作PM⊥CD于点M,QN⊥CD于点N,根据dE-CD=
,由②可得,t=2.4;当PQ与AB不平行时,过点P,Q分别作PM⊥CD于点M,QN⊥CD于点N,根据dE-CD=![]() ,dP-CA+dQ-CB=m,推理可得△PME≌△QNE,即可得出PM=QN,最后根据PM=PC×sin∠ACD=2t×sin∠B=
,dP-CA+dQ-CB=m,推理可得△PME≌△QNE,即可得出PM=QN,最后根据PM=PC×sin∠ACD=2t×sin∠B=![]() ,QN=QC×sin∠BCD=(6-t)sin∠A=
,QN=QC×sin∠BCD=(6-t)sin∠A=![]() (6-t),得到关于t的方程
(6-t),得到关于t的方程![]() ,即可得出t=
,即可得出t=![]() .
.
详解:(1)∵点C在线段AB上,若dC﹣AB=![]() ,
,
∴AC=![]() AB,即
AB,即![]() =
=![]() ;
;
∵AC=3BC,
∴AC=![]() AB,即dC﹣AB=
AB,即dC﹣AB=![]() ,
,
故答案为:![]() ,
,![]() ;
;
(2)①在△ABC中,∠ACB=90°,AB=10,BC=6,
∴AC=8,
∵dP﹣CA=![]() =
=![]() ,dQ﹣CB=
,dQ﹣CB=![]() =1﹣
=1﹣![]() ,
,
∴m=dP﹣CA+dQ﹣CB=![]() +1﹣
+1﹣![]() ,
,
又∵![]() ≤m≤
≤m≤![]() ,
,
∴![]() ≤
≤![]() +1﹣
+1﹣![]() ≤
≤![]() ,
,
解得3≤t≤4;
②∵dP﹣CA=![]() ,dP﹣CA+dQ﹣CB=m,
,dP﹣CA+dQ﹣CB=m,
∴dP﹣CA=dQ﹣CB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=2.4,
∵![]() =
=![]() ,∠ACB=∠PCQ,
,∠ACB=∠PCQ,
∴△ACB∽△PCQ,
∴∠A=∠CPQ,
∴PQ∥AB,
∴![]() =
=![]() ,
,
∴dE﹣CD=dP﹣CA=![]() =0.6;
=0.6;
③分两种情况:
当PQ∥AB时,则有dE﹣CD=dP﹣CA=dQ﹣CB=![]() ,
,
由②可得,t=2.4;
当PQ与AB不平行时,过点P,Q分别作PM⊥CD于点M,QN⊥CD于点N,如图所示,
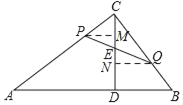
则有PM∥QN∥AB,且点M,N,E不重合,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∵dE﹣CD=![]() ,dP﹣CA+dQ﹣CB=m,
,dP﹣CA+dQ﹣CB=m,
∴dP﹣CA+dQ﹣CB=2dE﹣CD,
∴![]() +
+![]() =2
=2![]() ,即
,即![]() +
+![]() =2
=2![]() ,
,
∴CM+CN=2CE,即点E是MN的中点,
∴EN=EM,
又∵∠PME=∠QNE,∠PEM=∠QEN,
∴△PME≌△QNE,
∴PM=QN,
∵PM=PC×sin∠ACD=2t×sin∠B=![]() ,QN=QC×sin∠BCD=(6﹣t)sin∠A=
,QN=QC×sin∠BCD=(6﹣t)sin∠A=![]() (6﹣t),
(6﹣t),
∴![]() =
=![]() (6﹣t),
(6﹣t),
解得t=![]() ,
,
综上所述,t的值为2.4或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据: ![]() ≈1.414,、
≈1.414,、![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,文具店老板购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 14 |
B型 | 15 | 22 |
(1)老板如何进货,能使进货款恰好为1350元?
(2)要使销售文具所获利润不少于500元,那么老板最多能购进A型文具多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为18cm2,则S△DGF等于( )
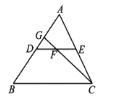
A.4cm2B.5cm2C.6cm2D.7 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
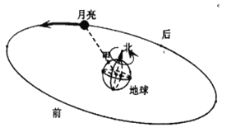
【题目】如果把月亮绕地球旋转的轨迹看成一个圆,地心在圆心上。我们知道地球每24小时逆时针方向自转一圈(从俯视角度看),月亮每月逆时针绕地球旋转一圈.
(1)求地球每小时旋转的角度;
(2)求月亮绕地球每小时旋转的角度(每月以30天记);
(3)某月15日20:00时,月亮恰好在甲地正上方(如图),到第二天大约几时几分月亮再次出现在甲地正上方?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;
(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
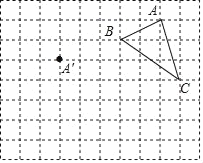
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
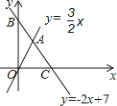
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于点A.
相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线![]() 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“很了解”部分所对应扇形的圆心角为_______;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com