
【题目】童星玩具厂工人的工作时间为:每月22天,每天8小时.工资待遇为:按件计酬,多劳多得,每月另加福利工资500元,按月结算.该厂生产A、B两种产品,工人每生产一件A种产品可得报酬1.50元,每生产一件B种产品可得报酬2.80元.该厂工人可以选择A、B两种产品中的一种或两种进行生产.工人小李生产1件A产品和1件B产品需35分钟;生产3件A产品和2件B产品需85分钟.
(1)小李生产1件A产品需要 分钟,生产1件B产品需要 分钟.
(2)求小李每月的工资收入范围.
【答案】(1)![]() ;(2) 不低于1556元而不高于1978.4元.
;(2) 不低于1556元而不高于1978.4元.
【解析】分析:
(1)设小李每生产一件A种产品、每生产一件B种产品分别需要x分钟和y分钟,根据题意列出方程组,解方程组即可求得所求答案;
(2)设小李每个月生产A种产品a件,工资收入为w元,根据题意列出w和a之间的函数关系式,将所列函数关系式化简后即可由w随a变化而变化的趋势结合题中已知量求得所求答案了.
解:(1)设小李每生产一件A种产品、每生产一件B种产品分别需要x分钟和y分钟,根据题意,得
![]() ,解得:
,解得:![]() ,
,
答:小李生产1件A种产品需15分子,生产1件B种产品,需20分钟;
(2)设小李每个月生产A种产品a件,工资收入为w元,根据题意可得:w=500+1.5a+2.8(22×8×60﹣15a)÷20,
整理得w=﹣0.6a+1978.4,
∴w随a的增大而减小,
当小李该月只生产A种产品时,其工资收入最低,最低收入为:
w=-0.6 (22×8×60÷15) +1978.4=1556(元);
当小李该月只生产B中产品时,其工资收入最高,最高为:
w=-0.6×0+1978.4=1978.4(元);
故小李每月的工资数目不低于1556元而不高于1978.4元.


科目:初中数学 来源: 题型:
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为18cm2,则S△DGF等于( )
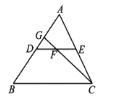
A.4cm2B.5cm2C.6cm2D.7 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;
(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
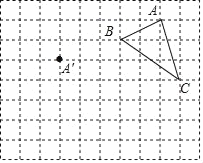
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)=![]() =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
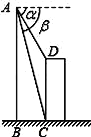
查看答案和解析>>
科目:初中数学 来源: 题型:
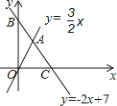
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于点A.
相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线![]() 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
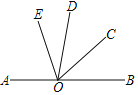
【题目】如图,点O在直线AB上,∠AOC与∠COD互补,OE平分∠AOC.
(1)若∠BOC=40°,则∠DOE的度数为 ;
(2)若∠DOE=48°,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() 是关于
是关于![]() 的函数,
的函数,![]() 是常数(
是常数(![]() ),若对于此函数图象上的任意两点
),若对于此函数图象上的任意两点![]() ,
,![]() ,都有
,都有![]() ,则称该函数为有界函数,其中满足条件的所有常数
,则称该函数为有界函数,其中满足条件的所有常数![]() 的最小值,称为该函数的界高.
的最小值,称为该函数的界高.
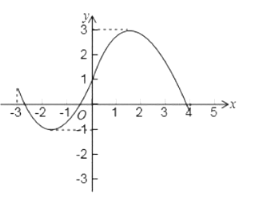
例如:下图所表示的函数的界高为4.
(1)求函数![]() 的界高;
的界高;
(2)已知![]() ,若函数
,若函数![]() 的界高为4,求实数
的界高为4,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() ,函数
,函数![]() 的界高为
的界高为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com