
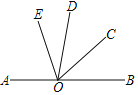
【题目】如图,点O在直线AB上,∠AOC与∠COD互补,OE平分∠AOC.
(1)若∠BOC=40°,则∠DOE的度数为 ;
(2)若∠DOE=48°,求∠BOD的度数.
【答案】(1)30°;(2)56°
【解析】
(1)根据互补的关系和邻补角以及角平分线的定义解答即可;
(2)设∠BOC为x,根据互补的关系和角平分线的定义表示出∠COD,∠AOE、∠EOC,列出方程解答即可.
解:(1)∵点O在直线AB上,∠BOC=40°,
∴∠AOC=140°,
∵∠AOC与∠COD互补,
∴∠COD=40°,
∵OE平分∠AOC,
∴∠EOC=70°,
∴∠DOE=∠EOC -∠COD =70°-40°=30°;
故答案为:30°;
(2)∵点O在直线AB上,
∴∠AOC与∠BOC互补,
∵∠AOC与∠COD互补,
∴∠BOC=∠COD,
∵OE平分∠AOC,
∴∠AOE=∠EOC,
设∠BOC为x,则∠COD=x,∠AOE=∠EOC=48°+x,
可得:2(48°+x)+x=180°,
解得:x=28°,
∴∠BOD=2∠BOC=56°.
故答案为:56°.


科目:初中数学 来源: 题型:
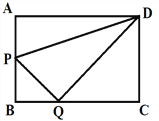
【题目】在矩形ABCD中,AB=3,AD=4,动点P从点B出发,以每秒1个单位的速度,沿BA向点A移动;同时点Q从点C出发,以每秒2个单位的速度,沿CB向点B移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤2),解答下列问题:
(1)当x为何值时,PQ⊥DQ;
(2)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最小值?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】童星玩具厂工人的工作时间为:每月22天,每天8小时.工资待遇为:按件计酬,多劳多得,每月另加福利工资500元,按月结算.该厂生产A、B两种产品,工人每生产一件A种产品可得报酬1.50元,每生产一件B种产品可得报酬2.80元.该厂工人可以选择A、B两种产品中的一种或两种进行生产.工人小李生产1件A产品和1件B产品需35分钟;生产3件A产品和2件B产品需85分钟.
(1)小李生产1件A产品需要 分钟,生产1件B产品需要 分钟.
(2)求小李每月的工资收入范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.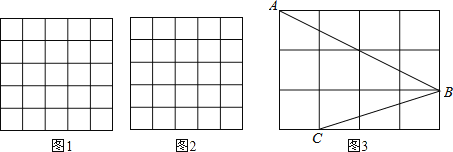
查看答案和解析>>
科目:初中数学 来源: 题型:
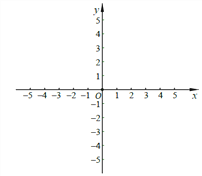
【题目】已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4的图像经过A(-2,0)、
B(4,0)两点,与y轴交于点C点.
(1)求这个二次函数的解析式;
(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;
(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图像的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有![]() 、
、![]() 、
、![]() 、
、![]() 四个点,分别对应
四个点,分别对应![]() ,
,![]() ,
,![]() ,
,![]() 四个数,其中
四个数,其中![]() ,
,![]() ,
,![]() 与
与![]() 互为相反数,
互为相反数,
![]()
(1)求![]() ,
,![]() 的值;
的值;
(2)若线段![]() 以每秒3个单位的速度,向右匀速运动,当
以每秒3个单位的速度,向右匀速运动,当![]() _______时,点
_______时,点![]() 与点
与点![]() 重合,当
重合,当![]() _______时,点
_______时,点![]() 与点
与点![]() 重合;
重合;
(3)若线段![]() 以每秒3个单位的速度向右匀速运动的同时,线段
以每秒3个单位的速度向右匀速运动的同时,线段![]() 以每秒2个单位的速度向左匀速运动,则线段
以每秒2个单位的速度向左匀速运动,则线段![]() 从开始运动到完全通过
从开始运动到完全通过![]() 所需时间多少秒?
所需时间多少秒?
(4)在(3)的条件下,当点![]() 运动到点
运动到点![]() 的右侧时,是否存在时间
的右侧时,是否存在时间![]() ,使点
,使点![]() 与点
与点![]() 的距离是点
的距离是点![]() 与点
与点![]() 的距离的4倍?若存在,请求出
的距离的4倍?若存在,请求出![]() 值,若不存在,请说明理由.
值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
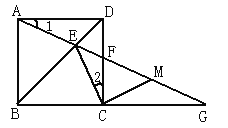
【题目】如图,正方形ABCD中,E是BD上一点,AE的延长线交CD于F,交BC的延长线于G,M是FG的中点.
(1)求证:① ∠1=∠2;② EC⊥MC.
(2)试问当∠1等于多少度时,△ECG为等腰三角形?请说明理由.
【答案】(1)①证明见解析;②证明见解析;(2)当∠1=30°时,△ECG为等腰三角形. 理由见解析.
【解析】试题分析:(1)①根据正方形的对角线平分一组对角可得![]() 然后利用边角边定理证明
然后利用边角边定理证明![]() ≌
≌![]() 再根据全等三角形对应角相等即可证明;
再根据全等三角形对应角相等即可证明;
②根据两直线平行,内错角相等可得![]() 再根据直角三角形斜边上的中线等于斜边的一半可得
再根据直角三角形斜边上的中线等于斜边的一半可得![]() 然后据等边对等角的性质得到
然后据等边对等角的性质得到![]() ,所以
,所以![]() 然后根据
然后根据![]() 即可证明
即可证明![]() 从而得证;
从而得证;
(2)根据(1)的结论,结合等腰三角形两底角相等![]() 然后利用三角形的内角和定理列式进行计算即可求解.
然后利用三角形的内角和定理列式进行计算即可求解.
试题解析:(1)证明:①∵四边形ABCD是正方形,
∴∠ADE=∠CDE,AD=CD,
在△ADE与△CDE,
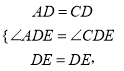
∴△ADE≌△CDE(SAS),
∴∠1=∠2,
②∵AD∥BG(正方形的对边平行),
∴∠1=∠G,
∵M是FG的中点,
∴MC=MG=MF,
∴∠G=∠MCG,
又∵∠1=∠2,
∴∠2=∠MCG,
∵![]()
∴![]()
∴EC⊥MC;
(2)当∠1=30°时, ![]() 为等腰三角形. 理由如下:
为等腰三角形. 理由如下:
∵![]() 要使
要使![]() 为等腰三角形,必有
为等腰三角形,必有![]()
∴![]() span>
span>
∵![]()
∴![]()
∴![]()
∴∠1=30°.
【题型】解答题
【结束】
24
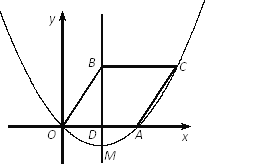
【题目】如图,已知抛物线经过原点O和点A,点B(2,3)是该抛物线对称轴上一点,过点B作BC∥x轴交抛物线于点C,连结BO、CA,若四边形OACB是平行四边形.
(1)① 直接写出A、C两点的坐标;② 求这条抛物线的函数关系式;
(2)设该抛物线的顶点为M,试在线段AC上找出这样的点P,使得△PBM是以BM为底边的等腰三角形并求出此时点P的坐标;
(3)经过点M的直线把□ OACB的面积分为1:3两部分,求这条直线的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com