
【题目】若二次函数y=ax2+bx﹣4的图象开口向上,与x轴的交点为(4,0)、(﹣2,0),则当x1=﹣1,x2=2时,对应的函数值y1和y2的大小关系为( )
A. y1>y2 B. y1=y2 C. y1<y2 D. 不确定
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若a+b=2,则称a与b是关于1的平衡数.
(1)①3与 是关于1的平衡数;②4﹣x与 是关于1的平衡数(用含x的代数式表示).
(2)若a=2x2﹣3(x2+x)﹣4,b=2x﹣[3x﹣(4x+x2)﹣2],判断a与b是否是关于1的平衡数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校羽毛球队需要购买6支羽毛球拍和x盒羽毛球,羽毛球拍市场价为200元/支,羽毛球为30元/盒.甲商场优惠方案为:所有商品9折.乙商场优惠方案为:买1支羽毛球拍送1盒羽毛球,其余原价销售.
![]() 当
当![]() 大于
大于![]() 时,分别用含
时,分别用含![]() 的代数式表示在甲商场和乙商场购买所有物品的费用.
的代数式表示在甲商场和乙商场购买所有物品的费用.
![]() 当
当![]() 时,请你通过计算说明选择哪个商场购买比较省钱.
时,请你通过计算说明选择哪个商场购买比较省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
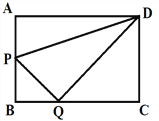
【题目】在矩形ABCD中,AB=3,AD=4,动点P从点B出发,以每秒1个单位的速度,沿BA向点A移动;同时点Q从点C出发,以每秒2个单位的速度,沿CB向点B移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤2),解答下列问题:
(1)当x为何值时,PQ⊥DQ;
(2)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最小值?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且CB=5米.

(1)求钢缆CD的长度;(精确到0.1米)
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
(参考数据:tan400=0.84, sin400=0.64, cos400=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】日历上的规律:表格是2020年元月的日历,图中的阴影区域是在日历中选取的一块九宫格.
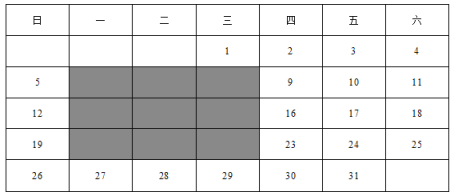
(1)九宫格中,四个角的四个数之和与九宫格中央那个数有什么关系?
(2)请你自选一块九宫格进行计算,看四个角上的四个数之和与九宫格中央那个数是否还有这种关系?
(3)试说明原理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4的图像经过A(-2,0)、
B(4,0)两点,与y轴交于点C点.
(1)求这个二次函数的解析式;
(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;
(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图像的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com