
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.

(1)求证:BE是⊙O的切线;
![]() (2)若BC=
(2)若BC=![]() ,AC=5,求圆的直径AD及切线BE的长.
,AC=5,求圆的直径AD及切线BE的长.
【答案】(1)详见解析;(2)R=3,BE=![]() .
.
【解析】
试题分析:(1)连接OB,根据已知条件易证∠EBD=∠CAB,继而得到∠BAD=∠EBD,根据直径所对的圆周角为直角即可证得结论;(2)连接CD,交OB于点F,易证OF为三角形ADC的中位线,根据三角形的中位线定理求得OF,再用平行线分线段成比例定理求出半径R,最后用切割线定理即可.
试题解析:(1)如图,
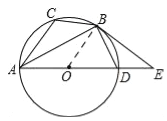
连接OB,∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是⊙O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在⊙O上,
∴BE是⊙O的切线,
(2)如图2,
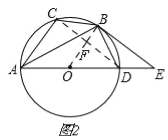
设圆的半径为R,连接CD,
∵AD为⊙O的直径,
∴∠ACCD=90°,
∵BC=BD,
∴OB⊥CD,
∴OB∥AC,
∵OA=OD,
∴OF=![]() AC=
AC=![]() ,
,
∵四边形ACBD是圆内接四边形,
∴∠BDE=∠ACB,
∵∠DBE=∠ACB,
∴△DBE∽△CAB,
∴![]() ,
,
即![]() ,
,
∴DE=![]() ,
,
∵∠OBE=∠OFD=90°,
∴DF∥BE,
∴![]() ,
,
∴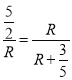 ,
,
∵R>0,
∴R=3,
∵BE是⊙O的切线,
∴BE=![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 要了解一批灯泡的使用寿命应采用普方式
B. “任意画出一个等边三角形,它是轴对称图形”是随机事件
C. 有一组数据:3,5,7,6,4,这组数据的中位数是5.
D. 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会关注.“寒假”期间,记者小刘随机调查了某区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:
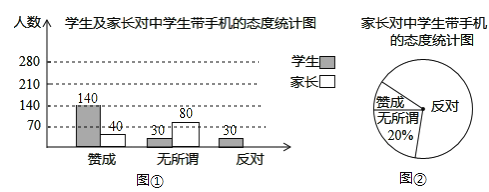
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)若该区共有中学生8000人,请根据以上图表信息估算出该区中学生中对“校园手机”持“无所谓”态度的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com