
����Ŀ��ij��ѧ���������40�����ʵ��������ij��˾����һ�Ҽ��˵꾭Ӫ���˽һ�ֳɱ�Ϊ20Ԫ/����������Ʒ�ڵ�![]() �����۵������Ϣ���±���ʾ��
�����۵������Ϣ���±���ʾ��
������ |
|
���۵��� | �� �� |
��1�������ڼ������Ʒ�����۵���Ϊ35Ԫ/����
��2����40���иü��˵�ڼ����õ����������������Ƕ��٣�
��3����ʵ�����۵�ǰ20���У���˾Ϊ�������˵���մ�ѧ���μ�ʵ�������ÿ����һ����Ʒ�ͷ����ü��˵�![]() Ԫ������ͨ���ü��˵�����ۼ�¼���֣�ǰ10���У�ÿ���ý������������ʱ��
Ԫ������ͨ���ü��˵�����ۼ�¼���֣�ǰ10���У�ÿ���ý������������ʱ��![]() ���죩�������������
���죩�������������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��10��35����2����21��ʱ�����������������Ϊ725����3��![]() ��
��
��������
��1����������㣬��![]() ʱ�͵�
ʱ�͵�![]() ʱ�ĺ���ֵΪ35��Ȼ����ö�Ӧ��x��ֵ���ɣ�
ʱ�ĺ���ֵΪ35��Ȼ����ö�Ӧ��x��ֵ���ɣ�
��2����Ϊ��![]() ʱ�͵�
ʱ�͵�![]() ʱ����������г��������ĺ�����ϵʽ��Ȼ�����ö��κ����ͷ�����������������⼴�ɣ�
ʱ����������г��������ĺ�����ϵʽ��Ȼ�����ö��κ����ͷ�����������������⼴�ɣ�
��3������������ߵĶԳ��᷽�̣�Ȼ������ǰ10���������x������������г�����m�IJ���ʽ��⼴�ɣ�
�⣺��1����![]() ʱ��
ʱ��![]() �����
�����![]()
��![]() ʱ��
ʱ��![]() �����
�����![]() ��
��
�𣺵�10���35��ʱ������Ʒ���۵���Ϊ35Ԫ/����
�ʴ�Ϊ��10��35��
��2����![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() �����ֵΪ612.5
�����ֵΪ612.5
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() �����ֵΪ725��
�����ֵΪ725��
��![]() ��
��
���21��ʱ�����������������Ϊ725Ԫ��
�𣺵�21��ʱ�����������������Ϊ725Ԫ��
�ʴ�Ϊ��725��
��3��![]() ��
��
��ǰ10��ÿ���ý������������ʱ��![]() ���죩�����������
���죩�����������
��Գ���Ϊ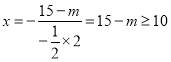 ����ã�
����ã�![]()
��![]() ��
��
��m��ȡֵ��ΧΪ��![]() ��
��
�ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
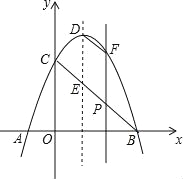
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=-x2+bx+c��x�ύ�ڵ�A��-1��0������B��3��0������y�ύ�ڵ�C���߶�BC�������ߵĶԳ��ύ�ڵ�E��PΪ�߶�BC�ϵ�һ�㣨�����B��C�غϣ�������P��PF��y�ύ�������ڵ�F������DF�����P�ĺ�����Ϊm��
��1���������������Ӧ�ĺ�������ʽ��
��2����PF�ij��ȣ��ú�m�Ĵ���ʽ��ʾ��
��3�����ı���PEDFΪƽ���ı���ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽����֪ʶ������Ч�������ȫУѧ��������һ�β��ԣ��������ȡ �˲���ѧ���IJ��Գɼ�(����100�֣���ͷ�Ϊ60�֣�80�ּ�����Ϊ����)��ͳ�ƺ���Ƴ����²�������

�����������Ϣ������������⣺
��1������![]() __________��
__________��![]() _________��
_________��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3������У��ѧ��2100�ˣ��Թ��Ʒ����ﵽ������ж����ˣ�
��4��ѧУ���ӵ÷���ߵ�5��ѧ��(3��2Ů)�У������ѡ2��ѧ��ȥ�μ�����ٰ�Ľ���֪ʶ������С��˵������Ϊ����������Ů��������![]() ��������ѡ�е�2��ѧ�����������ĸ�����ѡ�е�2��ѧ������Ů���ĸ��ʵ�
��������ѡ�е�2��ѧ�����������ĸ�����ѡ�е�2��ѧ������Ů���ĸ��ʵ�![]() ����������˵����ȷ�����жϲ�˵�����ɣ�
����������˵����ȷ�����жϲ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��ֱ��
��ֱ��![]() ���뾶
���뾶![]() ����
����![]() �ǰ�Բ
�ǰ�Բ![]() �����ȷֵ㣬��
�����ȷֵ㣬��![]() �ǰ뾶
�ǰ뾶![]() �ϵĶ��㣬ʹ
�ϵĶ��㣬ʹ![]() ��ֵ��Сʱ��
��ֵ��Сʱ��![]() �� ��
�� ��

A.1B.![]() C.2D.3
C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=BC��BD��AC�ڵ�D����FAC=![]() ��ABC���ҡ�FAC��AC�·�����P��Q�ֱ�������BD������AF�ϵĶ��㣬�ҵ�P�����B�غϣ���Q�����A�غϣ�����CQ������P��PE��CQ�ڵ�E������DE��
��ABC���ҡ�FAC��AC�·�����P��Q�ֱ�������BD������AF�ϵĶ��㣬�ҵ�P�����B�غϣ���Q�����A�غϣ�����CQ������P��PE��CQ�ڵ�E������DE��
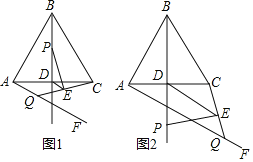
��1������ABC=60�㣬BP=AQ��
����ͼ1������P���߶�BD���˶�ʱ����ֱ��д���߶�DE���߶�AQ��������ϵ��λ�ù�ϵ��
����ͼ2������P�˶����߶�BD���ӳ�����ʱ�����жϢ��еĽ����Ƿ��������˵�����ɣ�
��2������ABC=2����60������ֱ��д�����߶�BP���߶�AQ����ʲô������ϵʱ����ʹ��1���ТٵĽ�����Ȼ�������ú��������Ǻ�����ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۵�����ABCD��ʹ��D����BC���ϵĵ�F����

��1����֤����ABF�ס�FCE��
��2����DC��8��CF��4�������ABCD�����S��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У�����y��![]() ��x��0����ͼ��G������A��4��1������ֱ��y��
��x��0����ͼ��G������A��4��1������ֱ��y��![]() x+b��ͼ���ڵ�B����y�ύ�ڵ�C�����кᡢ�����궼�������ĵ�������㣮��ͼ��G�ڵ�A��B֮��IJ������߶�OA��OC��BCΧ�ɵ��������߽磩ΪW����W��ǡ��4�����㣬��Ϻ���ͼ��b��ȡֵ��Χ�ǣ�������
x+b��ͼ���ڵ�B����y�ύ�ڵ�C�����кᡢ�����궼�������ĵ�������㣮��ͼ��G�ڵ�A��B֮��IJ������߶�OA��OC��BCΧ�ɵ��������߽磩ΪW����W��ǡ��4�����㣬��Ϻ���ͼ��b��ȡֵ��Χ�ǣ�������
A.��![]() ��b��1��
��b��1��![]() ��b��
��b��![]() B.��
B.��![]() ��b��1��
��b��1��![]() ��b��
��b��![]()
C.��![]() ��b����1��
��b����1��![]() ��b��
��b��![]() D.��
D.��![]() ��b����1��
��b����1��![]() ��b��
��b��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������50�����乩�ο;�ס����ÿ�����䶨��120Ԫʱ�������ȫ��ס������ÿ������ÿ��Ķ���ÿ����10Ԫʱ���ͻ���һ��������С�����ο;�ס���䣬�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã���ÿ�����䶨������10 xԪ��xΪ��������
��1����2�֣�ֱ��д��ÿ���ο;�ס�ķ�������y��x�ĺ�����ϵʽ��
��2����4�֣������ÿ�������ΪWԪ����ÿ�䷿�۶���Ϊ����Ԫʱ������ÿ���������������������Ƕ��٣�
��3����4�֣�ij�գ������˽���ס��������õ�������Ϣ������������������5000Ԫ��������Ϊ�ο;�ס�ķ��乲֧������û�г���600Ԫ����ÿ������պ�ס��2�ˡ��ʣ����������ס���ο����������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧϰ��һ�κ�����ʱ���۵ľ���ͷ����о�����![]() ��ͼ������ʣ���������⣮
��ͼ������ʣ���������⣮
![]() ������в��裬��������
������в��裬��������![]() ��ͼ��
��ͼ��
![]() �б�����գ�
�б�����գ�
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
![]() ��㣺
��㣺
![]() ����
����
![]() �۲�ͼ��x______ʱ��y��x�����������
�۲�ͼ��x______ʱ��y��x�����������
![]() ���ͼ����ʽ
���ͼ����ʽ![]() �Ľ⼯Ϊ______��
�Ľ⼯Ϊ______��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com