
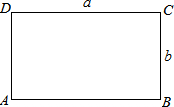
 如图,长方形ABCD的长AB、宽CB分别为a米、b米,a、b满足2|a-4|+|b-2|=0,一动点P从A出发以1米/秒的速度沿A→D→C→B→A运动,另一动点Q从B出发以2米/秒的速度沿B→C→D→A→B运动,设P、Q同时出发,运动的时间为t.
如图,长方形ABCD的长AB、宽CB分别为a米、b米,a、b满足2|a-4|+|b-2|=0,一动点P从A出发以1米/秒的速度沿A→D→C→B→A运动,另一动点Q从B出发以2米/秒的速度沿B→C→D→A→B运动,设P、Q同时出发,运动的时间为t.分析 (1)根据非负数,几个非负数的和是0,则每个数等于0,即可求得a和b的值;
(2)根据P和Q的位置对t进行讨论,然后利用三角形的面积公式求解;
(3)求出点Q运动到距离A点$\frac{1}{3}$米处时需要的时间t,求得DP的长,然后利用勾股定理求解.
解答 解:(1)根据题意得:a-4=0且b-2=0,解得:a=4,b=2;
(2)当0≤t≤1时,P在AD上,Q在BC上,AQ=t(米).
则S△APQ=$\frac{1}{2}$×t×4=2t;
当1<t≤2时,P在AD上,Q在CD上,CQ=2t-2,则S△APQ=$\frac{1}{2}$×t×(2t-2)=t2-t;
当2<t<$\frac{8}{3}$时,P和Q都在CD上,P在Q的左边,DP=t-2,CQ=2t-2,则PQ=4-(t-2)-(2t-2)=8-3t,S△APQ=$\frac{1}{2}$×2(8-3t)=8-3t;
当$\frac{8}{3}$≤t≤3时,P和Q都在CD上,P在Q的右边,DP=t-2,CQ=2t-2,则PQ=(t-2)+(2t-2)-4=3t-8,S△APQ=$\frac{1}{2}$×2(3t-8)=3t-8;
当3<t≤4时,P在CD上,Q在AD上,AQ=8-2t,DP=6-2t,则S△APQ=$\frac{1}{2}$×(8-2t)×(6-2t)=2t2-14t+24;
当4<t≤6时,Q在AB上,P在CD上,AQ=12-2t,则S△APQ=$\frac{1}{2}$×2×(12-2t)=12-2t;
当6≤t≤8时,Q在B点,BP=8-t,则S△APQ=$\frac{1}{2}$×4×(8-t)=16-2t;
当8≤t≤12时,Q在B点,P在AB上,PQ=t-8,则S△APQ=$\frac{1}{2}$×2×(t-8)=t-8;
(3)点Q运动到距离A点$\frac{1}{3}$米处时,Q在AD上,运动的时间是$\frac{8-\frac{1}{3}}{2}$=$\frac{23}{6}$(秒),
当P运动$\frac{23}{6}$秒时,DP=$\frac{23}{6}$-2=$\frac{11}{6}$(米).
则PA=$\sqrt{{2}^{2}+(\frac{11}{6})^{2}}$=$\frac{\sqrt{265}}{6}$(米).
点评 本题考查了矩形的性质,以及三角形的面积公式,根据P和Q的位置对t进行正确讨论是关键.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
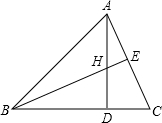 如图,H是△ABC的高AD、BE的交点,且DH=DC.给出下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD.其中正确的是( )
如图,H是△ABC的高AD、BE的交点,且DH=DC.给出下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD.其中正确的是( )| A. | ①② | B. | ②③ | C. | ①④ | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com