练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

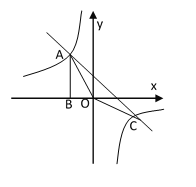
    【题目】如图，Rt△ABO的顶点A是双曲线与直线在第二象限的交点，AB⊥轴于B，且.

    （1）求这两个函数的解析式；

    （2）求△AOC的面积.

    【答案】（1）y=；（2）4.

    【解析】

    （1）先根据反比例函数的图象所在的象限判断出k的符号，再由△ABO的面积求出k的值，进而可得出两个函数的解析式；
    （2）先把两函数的解析式联立组成方程组，求出x、y的值，得出A、C两点的坐标，再由一次函数的解析式求出直线与y轴的交点D的坐标，然后根据S△AOC=S△AOD+S△COD进行解答即可．

    解：(1)设A点坐标为（x,y）,且x<0,y>0

    ∵

    ∴xy=-3，∴k=-3

    ∴y=

    (2)在y=-x+2中，当x=0时，y=2，

    ∴直线y=-x+2与y轴交点D为（0,2）

    由得，

    ∴A（-1,3），C（3，-1）

    ∴

    =

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点A的坐标为(3, 2)，点B的坐标为(3, 0). 作如下操作:①以点A为旋转中心，把△ABO顺时针旋转90°，得到△ACD;

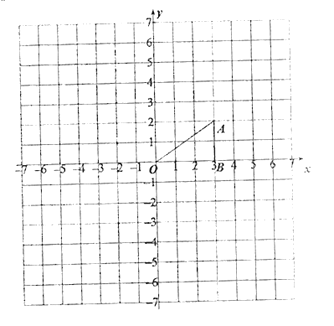
    (1)在图中画出△ACD;

    (2)①请直接写点B旋转到点C的路径长:____________；

    ②画出△ABO关于点O的中心对称图形△EOF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠C＝90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．

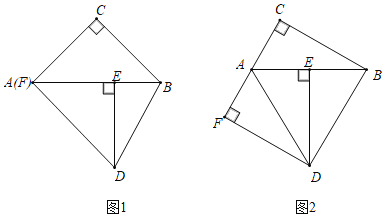
    （1）如图1，若点F与点A重合，求证：AC＝BC．

    （2）如图2，若点F在线段CA的延长线上，∠DAF＝∠DBA，请判断线段AF与BE的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知BD是矩形ABCD的对角线，AB＝20厘米，BC＝40厘米．点P、Q同时从点A出发，分别以2厘米/秒、4厘米/秒的速度由A→B→C→D→A的方向在矩形边上运动，只要Q点回到点A，运动全部停止．设运动时间为t秒．

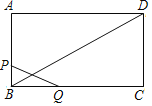
    （1）当点P运动在AB（含B点）上，点Q运动在BC（含B、C点）上时，

    ①设PQ的长为y，求y关于时间t的函数关系式，并写出t的取值范围？

    ②当t为何值时，△DPQ是等腰三角形？

    （2）在P、Q的整个运动过程中，分别判断下列两种情形是否存在？如果存在，请求出t的值；如果不存在，请说明理由．

    ①PQ与BD平行；

    ②PQ与BD垂直．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

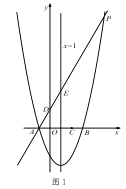
    【题目】如图1，对称轴为直线x=1的抛物线y=x2+bx+c，与x轴交于A、B两点（点A在点B的左侧），且点A坐标为(-1，0).又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与抛物线对称轴交于点E，点C与坐标原点O关于该对称轴成轴对称.

    （1）求点 B 的坐标和抛物线的表达式；

    （2）当 AE：EP=1：4 时，求点 E 的坐标；

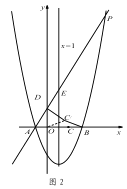
    （3）如图 2，在（2）的条件下，将线段 OC 绕点 O 逆时针旋转得到 OC ′，旋转角为 α(0°＜α＜90°)，连接 C ′D、C′B，求 C ′B+ C′D 的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC三个顶点的坐标分别为A（﹣1，﹣1）、B（﹣3，﹣2）C（0，﹣3）

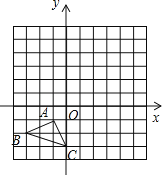
    （1）以点C为旋转中心将△ABC顺时针旋转90°，得到△A1B1C1，则A1的坐标为　 　；

    （2）以点O为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画出△A2B2C2；

    （3）若网格单位长度为1，求（1）中AB扫过的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一元二次方程：M：ax2+bx+c=0； N：cx2+bx+a=0，其中ac≠0，a≠c，以下四个结论：

    ①如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根；

    ②如果方程M有两根符号相同，那么方程N的两根符号也相同；

    ③如果m是方程M的一个根，那么是方程N的一个根；

    ④如果方程M和方程N有一个相同的根，那么这个根必是x=1

    正确的个数是（　　）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2018年12月4日是第五个国家宪法日，也是第一个“宪法宣传周”．甲、乙两班各选派10名学生参加宪法知识竞赛（满分100分），成绩如下：

    成绩

    85

    90

    95

    100

    甲班参赛学生/人

    1

    1

    5

    3

    乙班参赛学生/人

    1

    2

    3

    4

    分别求甲、乙两班参赛学生竞赛成绩的平均数和方差．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形中，，点、分别在、上，，，则的面积是________．

    查看答案和解析>>

    同步练习册答案