
【题目】已知直线![]() 与x轴和y轴分别交于点A和点B,抛物线
与x轴和y轴分别交于点A和点B,抛物线![]() 的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
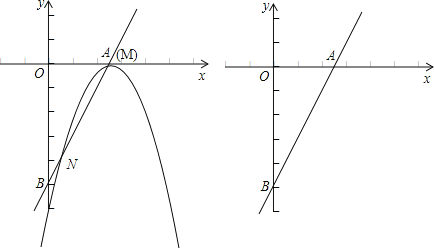
(1)如图,当点M与点A重合时,求:
①抛物线的解析式;
②点N的坐标和线段MN的长;
(2)抛物线![]() 在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)①![]() ②N(
②N(![]() ,-4),
,-4),![]() (2)存在.点M的坐标为(2,-1)或(4,3)
(2)存在.点M的坐标为(2,-1)或(4,3)
【解析】
(1)①由直线![]() 与x轴和y轴分别交于点A和点B,求出点A、B的坐标,由顶点M与点A重合,根据二次函数的性质求出顶点解析式.
与x轴和y轴分别交于点A和点B,求出点A、B的坐标,由顶点M与点A重合,根据二次函数的性质求出顶点解析式.
②联立![]() 和
和![]() ,求出点N的坐标,过N作NC⊥x轴,由勾股定理求出线段MN的长.
,求出点N的坐标,过N作NC⊥x轴,由勾股定理求出线段MN的长.
(2)根据相似三角形的性质,可得关于m或n的方程,可得M点的坐标,要分类讨论,以防遗漏.
解:(1)①∵直线![]() 与x轴和y轴分别交于点A和点B,
与x轴和y轴分别交于点A和点B,
∴A(![]() ,0),B(0,-5).
,0),B(0,-5).
当顶点M与点A重合时,∴M(![]() ,0).
,0).
∴抛物线的解析式是:![]() ,即
,即![]() .
.
②∵N是直线![]() 与在抛物线
与在抛物线![]() 的交点,
的交点,
∴ ,解得
,解得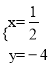 或
或![]() .
.
∴N(![]() ,-4).
,-4).
如图,过N作NC⊥x轴,垂足为C.
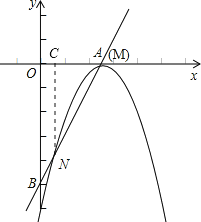
∵N(![]() ,-4),∴C(
,-4),∴C(![]() ,0)
,0)
∴NC=4.MC=OM-OC=![]() .
.
∴![]() .
.
(2)设M(m,2m-5),N(n,2n-5).![]() ,
,
![]() ,
,
则OB=2OA,![]() ,
,
当∠MON=90°时,
∵AB≠MN,且MN和AB边上的高相等,因此△OMN与△AOB不能全等,
∴△OMN与△AOB不相似,不满足题意.
当∠OMN=90°时,![]() ,即
,即![]() ,解得
,解得![]() ,
,
则m2+(2m-5)2=(![]() )2,解得m=2,
)2,解得m=2,
∴M(2,-1);
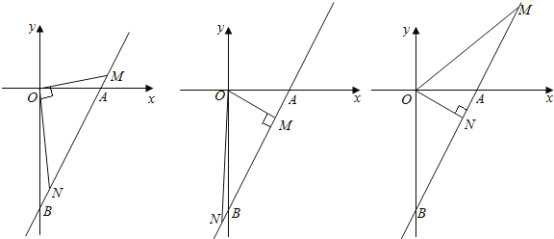
当∠ONM=90°时,![]() ,即
,即![]() ,解得
,解得![]() ,
,
则n2+(2n-5)2=(![]() )2,解得n=2,
)2,解得n=2,
解得:m=4,
则M的坐标是M(4,3).
故M的坐标是:(2,-1)或(4,3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
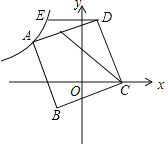
【题目】如图,在平面直角坐标系中,正方形ABCD顶点B(﹣1,﹣1),C在x轴正半轴上,A在第二象限双曲线y=﹣![]() 上,过D作DE∥x轴交双曲线于E,连接CE,则△CDE的面积为( )
上,过D作DE∥x轴交双曲线于E,连接CE,则△CDE的面积为( )
A.3B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
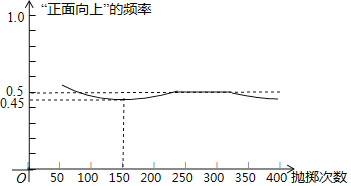
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,E,F在BC、CD上,以EF为直径的半圆切AD于G(如图1).
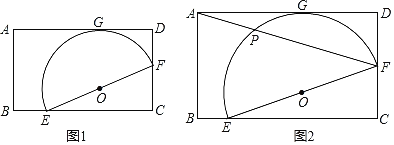
(1)求证:CE=2DG;
(2)若F为DC中点,连AF交半圆于P(如图2),且AB=4,AD=5![]() ,求PF.
,求PF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 ;

查看答案和解析>>
科目:初中数学 来源: 题型:
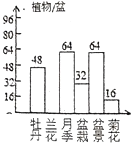
【题目】主题为“绿色生活,美丽家园”的世界园艺博览会,将于2019年4月29日至2019年10月7日在中国北京市延庆区举行.据介绍,在国际竞赛区,举办牡丹、兰花、月季、组合盆栽、盆景、菊花六类专项国际竞赛(参赛植物以盆为单位).
(1)求参加竞赛的共有多少盆植物?
(2)补全频数分布直方图;
(3)求“从参赛作品中任选一盆植物,是月季或盆栽”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)

(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
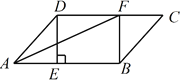
【题目】如图,在平行四边形![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com