
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )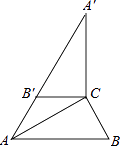
A.6
B.4 ![]()
C.3 ![]()
D.3
【答案】A
【解析】解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠CAB=30°,故AB=4,
∵△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,
∴AB=A′B′=4,AC=A′C,
∴∠CAA′=∠A′=30°,
∴∠ACB′=∠B′AC=30°,
∴AB′=B′C=2,
∴AA′=2+4=6.
故答案为:A.
根据含30![]() 角的直角三角形的边角关系得出AB的长,由旋转的性质得AB=A′B′=4,AC=A′C,根据等边对等角得出∠CAA′=∠A′=30°,进而得出∠ACB′=∠B′AC=30°,,根据等角对等边得出AB′=B′C=2,,从而得出AA的长。
角的直角三角形的边角关系得出AB的长,由旋转的性质得AB=A′B′=4,AC=A′C,根据等边对等角得出∠CAA′=∠A′=30°,进而得出∠ACB′=∠B′AC=30°,,根据等角对等边得出AB′=B′C=2,,从而得出AA的长。


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】某开发公司生产的 960 件新产品需要精加工后,才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用 20 天,而甲工厂每天加工的数量是乙工厂每天加工的数量的![]() ,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家合作完成.在加工过程中,公司派一名工程师每天到厂进行技术指导,并负担每天 15 元的午餐补助费, 请你帮公司选择一种既省时又省钱的加工方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习特殊的四边形,即平行四边形(继续学习它们的特殊类型如矩形、菱形等)来逐步认识四边形;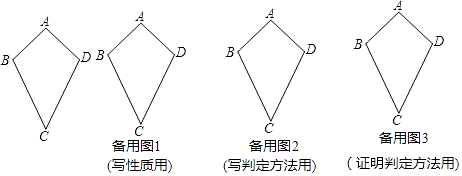
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年4月份的尼泊尔强震曾经导致珠峰雪崩,在珠峰抢险时,需8组登山队员步行运送物资,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人;若按每组人数比预定人数少分配1人,则总数不够90人,那么预定每组分配的人数是( )
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.(1)、求点A、B的坐标;(2)、已知点C(-2,2),求△BOC的面积;(3)、点P是第一象限角平分线上一点,若![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,在
,在![]() 的外部作等边三角形
的外部作等边三角形![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
①补全图2;
②若![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
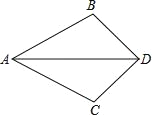
【题目】如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件________;
(2)根据“ASA”需添加条件________;
(3)根据“AAS”需添加条件________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com