练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，边长为6的正方形绕点按顺时针方向旋转后得到正方形，交于点，则____________．

    【答案】．

    【解析】

    过点F作FI⊥BC于点I，延长线IF交AD于J，根据含30°直角三角形的性质可求出FI、FJ和JH的长度，从而求出HD的长度．

    解：过点F作FI⊥BC于点BC，延长线AD交AD于J，

    由题意可知：CF=BC=6，∠FCB=30°，

    ∴FI=3，CI=

    ∵JI=CD=6，

    ∴JF=JI-FI=6-3=3，

    ∵∠HFC=90°，

    ∴∠JFH+∠IFC=∠IFC+∠FCB=90°，

    ∴∠JFH=∠FCB=30°，

    设JH=x，则HF=2x，

    ∴由勾股定理可知：（2x）2=x2+32，

    ∴x=，

    ∴DH=DJ-JH=

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：二次函数y=x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．

    （1）求抛物线的解析式；

    （2）抛物线的对称轴上有一动点P，求出PA+PD的最小值；

    （3）点G抛物线上的动点，在x轴上是否存在点E，使B、D、E、G这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的E点坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料题

    点A、B在数轴上分别表示实数、，A、B两点之间的距离记作AB. 当A、B两点中有一点为原点时，不妨设A点在原点。如下图①所示，则AB =OB =＝.

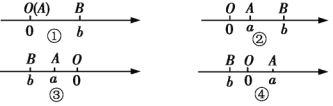
    当A、B两点都不在原点时：

    （1）上图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB－OA＝＝＝＝

    （2）上图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB－OA＝＝＝＝

    （3）如上图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB＋OA＝＝＝

    回答下列问题：

    ①综上所述，数轴上A、B两点之间的距离AB＝　　　　 　　.

    ②数轴上表示2和的两点A和B之间的距离AB＝　　　 　　　.

    ③数轴上表示x和的两点A和B之间的距离AB＝　　 　 　，如果AB＝2，则x的值为　　　 　.

    ④若代数式有最小值，则最小值为 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2017次运动后，动点P的坐标是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，平面直角坐标系x0y中，点A（0，2），B（1，0），C（﹣4，0）点D为射线AC上一动点，连结BD，交y轴于点F，⊙M是△ABD的外接圆，过点D的切线交x轴于点E．

    （1）判断△ABC的形状；

    （2）当点D在线段AC上时，

    ①证明：△CDE∽△ABF；

    ②如图2，⊙M与y轴的另一交点为N，连结DN、BN，当四边形ABND为矩形时，求tan∠DBC；

    （3）点D在射线AC运动过程中，若，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A（-3，-3），B（-2，-1），C（-1，-2）是直角坐标平面上的三点．

    （1）请画出△ABC关于x轴对称的△ABC；

    （2）请写出B点关于y轴对称的点B2的坐标；若将点B向上平移h个单位，欲使其落在△A1B1C1内部，指出h的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边的边长为，点从点出发沿向点运动，点从点出发沿的延长线向右运动，已知点，都以的速度同时开始运动，运动过程中与相交于点，点运动到点后两点同时停止运动．

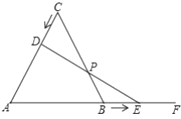
    （1）当是直角三角形时，求，两点运动的时间；

    （2）求证：在运动过程中，点始终是线段的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）请在横线上填写适当的内容，完成下面的解答过程：

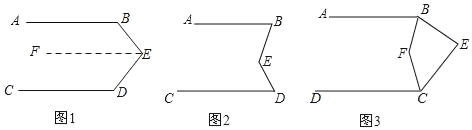
    如图①，如果∠ABE+∠BED+∠CDE＝360°，试说明AB∥CD．

    理由：过点E作EF∥AB

    所以∠ABE+∠BEF＝　 　°（　 　）

    又因为∠ABE+∠BED+∠CDE＝360°

    所以∠FED+∠CDE＝　 　°

    所以EF∥　 　.

    又因为EF∥AB,

    所以AB∥CD.

    （2）如图②，如果AB∥CD，试说明∠BED＝∠B+∠D．

    （3）如图③，如果AB∥CD，∠BEC＝α，BF平分∠ABE，CF平分∠DCE，则∠BFC的度数是　 　（用含α的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们约定：体重在选定标准的%（包含）范围之内时都称为“一般体重”．为了解某校七年级男生中具有“一般体重”的人数，我们从该校七年级男生中随机选出10名男生，测量出他们的体重（单位：kg），收集并整理得到如下统计表：

    男生序号

    ①

    ②

    ③

    ④

    ⑤

    ⑥

    ⑦

    ⑧

    ⑨

    ⑩

    体重（kg）

    45

    62

    55

    58

    67

    80

    53

    65

    60

    55

    根据以上表格信息解决如下问题:

    （1）将这组数据的三个统计量：平均数、中位数和众数填入下表：

    平均数

    中位数

    众数

    （2）请你选择其中一个统计量作为选定标准，说明选择的理由．并按此选定标准找出这10名男生中具有“一般体重”的男生．

    查看答案和解析>>

    同步练习册答案