
����Ŀ����1�����ں�������д�ʵ������ݣ��������Ľ����̣�
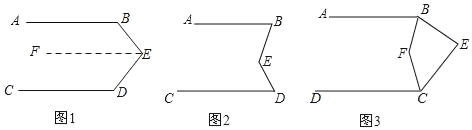
��ͼ���������ABE+��BED+��CDE��360�㣬��˵��AB��CD��
���ɣ�����E��EF��AB
���ԡ�ABE+��BEF���� ���㣨�� ����
������ABE+��BED+��CDE��360��
���ԡ�FED+��CDE���� ����
����EF���� ��.
����ΪEF��AB,
����AB��CD.
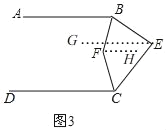
��2����ͼ�������AB��CD����˵����BED����B+��D��
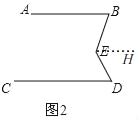
��3����ͼ�������AB��CD����BEC������BFƽ�֡�ABE��CFƽ�֡�DCE�����BFC�Ķ������� �����ú����Ĵ���ʽ��ʾ����
���𰸡���1��180����ֱ��ƽ�У�ͬ���ڽǻ�����180��CD����2������������3��180�㩁![]() ����
����
��������
��1�����жϳ���FED+��CDE=180���ó�EF��CD�����ɵó����ۣ�
��2�����жϳ���BEH=��B�����жϳ�EH��CD���ó���DEH=��D�����ɵĵó����ۣ�
��3�����жϳ���ABE+��DCE=360��-���������жϳ���ABF+��DCF=180��-![]() ����������2���Ľ��ۼ��ɵó����ۣ�
����������2���Ľ��ۼ��ɵó����ۣ�
��:��1������E��EF��AB
���ABE+��BEF��180���� ��ֱ��ƽ�У�ͬ���ڽǻ�����
�ߡ�ABE+��BED+��CDE��360��
���FED+��CDE��180��
��EF��CD
��EF��AB
��AB��CD��
�ʴ�Ϊ��180����ֱ��ƽ�У�ͬ���ڽǻ�����180��CD��
��2����ͼ2��
����E��EH��AB��
���BEH����B��
��EH��AB��AB��CD��
��EH��CD��
���DEH����D��
���BED����BEH+��DEH����B+��D��
��3����ͼ3��
����E��EG��AB��
���ABE+��BEG��180����
��EG��AB��CD��AB��
��EG��CD��
���DCE+��CEG��180��
���ABE+��BEG+��CEG+��DCE��360����
���ABE+��BEC+��DCE��360����
���ABE+��DCE��360������BEC��
�ߡ�BEC������
���ABE+��CCE��360��������
��BF��CF�ֱ�ƽ�֡�ABE����DCE��
���ABE��2��ABF����DCF��2��ECF��
���ABF+��DCF��180����![]() ����
����
����F����FH��AB��
ͬ��2���ķ����ã���BFC����ABF+��DCF��180����![]() ����
����
�ʴ�Ϊ��180����![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��4ac��b2��
������![]() ����������x1=��1��x2=3��
����������x1=��1��x2=3��
��3a+c��0
����y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3
����x��0ʱ��y��x���������
���н�����ȷ�ĸ����ǣ�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ6��������![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת
��˳ʱ�뷽����ת![]() ��õ�������
��õ�������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ____________��
____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ�����ڵȱ���ABC������M��BC���ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ�����ȱ���AMN������CN����֤����ACN=��ABC��
�����̽����
��2����ͼ�����ڵȱ���ABC������M��BC�ӳ����ϵ�����һ�㣨�����˵�C��������������������1���н��ۡ�ACN=��ABC����������˵��������
����չ���졿
��3����ͼ�����ڵ�����ABC����BA=BC����M��BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ����������AMN��ʹ���ǡ�AMN=��ABC������CN����̽����ABC���ACN��������ϵ����˵��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OE��AB��
��1������BOC��4��AOC�����BOD�Ķ�����
��2������1����2����OF��CD��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
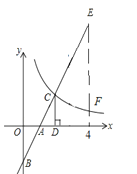
����Ŀ����ͼ����ֱ������ϵ�У�ֱ��y1=2x��2�������ύ��A��B���㣬��˫����y2=![]() ��x��0�����ڵ�C������C��CD��x�ᣬ����ΪD����OA=AD�������½��ۣ��ٵ�x��0ʱ��y1��x�����������y2��x���������С����
��x��0�����ڵ�C������C��CD��x�ᣬ����ΪD����OA=AD�������½��ۣ��ٵ�x��0ʱ��y1��x�����������y2��x���������С����![]() ���۵�0��x��2ʱ��y1��y2������ͼ����x=4ʱ��EF=4��������ȷ���۵ĸ����ǣ� ��
���۵�0��x��2ʱ��y1��y2������ͼ����x=4ʱ��EF=4��������ȷ���۵ĸ����ǣ� ��
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��

��1����֤����CBG�ա�CDG��
��2������HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У��ı���AEBD�ܷ�Ϊ���Σ�����ܣ��������H�����ꣻ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����������A�Ͽ�����ǰ�������������Ĵ���BC�������B��C����ĸ��Ƿֱ�Ϊ45����35������֪����BC�������ͬһˮƽ���ϣ��䳤��Ϊ100m���������������ĸ߶ȣ�������������������ο����ݣ�sin35��=0.57��cos35��=0.82��tan35��=0.70��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����·��A��B�������25 km��C��DΪ����ׯ��DA��AB�ڵ�A��CB��AB�ڵ�B����֪DA��16 km��CB��11 km������Ҫ����·AB�Ͻ�һ�����ز�Ʒ�չ�վE��ʹ��C��D���嵽Eվ�ľ�����ȣ���EվӦ������Aվ����km����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com